Содержание
- Процентные ставки и методы их начисления.
- ПРОЦЕНТНЫЕ СТАВКИ И МЕТОДЫ НАЧИСЛЕНИЯ ПРОЦЕНТОВ
- Отличие простых процентов от сложных
- Что такое простой процент
- Сложные проценты по вкладу
- В чем отличие
- Простые и сложные проценты — что это такое? Калькулятор сложных процентов от Вебинвеста
- Простые и сложные проценты
- Формулы сложных процентов по вкладам и примеры решения задач
- Калькулятор сложных процентов от Вебинвеста
- Понятие простого и сложного процента
- Разница между простым процентом и сложным процентом
- Ключевые различия между простым интересом и сложным интересом
Процентные ставки и методы их начисления.
Процентная ставка — относительная величина процентных платежей на заемный капитал за определенной период времени, как правило, за год.
По степени реагирования на изменение рыночного уровня процента различают фиксированные процентные ставки и плавающие.
Фиксированная процентная ставка — ставка, установленная на весь период пользования заемными средствами без права ее пересмотра.
Плавающая процентная ставка — ставка по средне- и долгосрочным кредитам, уровень которой колеблется в зависимости от конъюнктуры денежно-кредитного рынка.
В банковской практике существуют различные методы и способы начисления процентов.
Так, в банковской практике применяются простые и сложные проценты.
Простые проценты используются прежде всего при краткосрочном кредитовании, когда один раз в квартал или другой срок, определенный договором, производятся начисление процентов и выплата их кредитору.
Банк должен тщательно анализировать все моменты, которые могут в конечном итоге повлиять на прибыльность банковских операций. Например, необходимо учитывать характер инфляции и в этой связи определять, что целесообразнее для банка.
Возможны различные способы начисления процента: они определяются характером измерения количества дней пользования ссудой и продолжительностью года в днях (временной базы для расчета процентов). Так, число дней ссуды может определяться точно или приближенно, когда продолжительность любого полного месяца признается равной 30 дням. Временная база приравнивается либо к фактической продолжительности года (365 или 366 дней) или приближенно к 360 дням. Соответственно, применяют следующие варианты начисления сложных процентов:
Точные проценты с фактическим числом дней ссуды;этот способ дает самые точные результаты и применяется многими центральными и крупными коммерческими банками. Он характеризуется тем, что для расчета используется точное число дней ссуды, временная база равняется фактической продолжительности года.
Обыкновенные проценты с точным числом дней ссуды.
Обыкновенные проценты с приближенным числом дней ссуды.
Здесь продолжительность ссуды в днях определяется приближенно, временная база равна 360 дням. Считается, что точное число дней ссуды в большинстве случаев больше приближенного, поэтому и размер начисленных процентов с точным числом дней обычно больше, чем с приближенным.
Банковская практика в России предусматривает начисление процентов по привлеченным и размещенным средствам (за исключением долговых обязательств и операций с платежными картами) по первому способу, а именно — как точные проценты с фактическим числом дней ссуды. По векселям и депозитным сертификатам применяется способ начисления обыкновенных процентов с приближенным числом дней ссуды.
схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);
• схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);
• обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.
Схему простых процентов используют в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года.
В этом случае в качестве показателя n берут величину, характеризующую удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год).
Длина временных интервалов в расчетах может округляться: месяц — 30 дней; квартал — 90; полугодие — 180; год — 360 (или 365) дней.
Другой весьма распространенной операцией краткосрочного характера с использованием формулы простых процентов является операция по учету векселей банком. В этом случае пользуются формулами 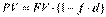 или
или 
где d — годовая дисконтная ставка в долях единицы;t — продолжительность финансовой операции в днях;Т — количество дней в году;f — относительная длина периода до погашения ссуды (отметим, что операция имеет смысл, когда число в скобках не отрицательно).Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этой ситуации капитал, генерирующий доходы, постоянно возрастает. Применяя простой процент, доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах либо в текущей деятельности.
ПРОЦЕНТНЫЕ СТАВКИ И МЕТОДЫ НАЧИСЛЕНИЯ ПРОЦЕНТОВ
ПРОЦЕНТНАЯ СТАВКА — относительная величина процентных платежей на заемный капитал за определенной период времени, как правило, за год.
По степени реагирования на изменение рыночного уровня процента различают фиксированные процентные ставки и плавающие.
ФИКСИРОВАННАЯ ПРОЦЕНТНАЯ СТАВКА — ставка, установленная на весь период пользования заемными средствами без права ее пересмотра. ,
ПЛАВАЮЩАЯ ПРОЦЕНТНАЯ СТАВКА — ставка по средне- и долгосрочным кредитам, уровень которой колеблется в зависимости от конъюнктуры денежно-кредитного рынка.
Плавающая процентная ставка складывается из двух составных частей. Первая часть представляет подвижную основу, изменяющуюся в соответствии с конъюнктурой денежно-кредитного рынка. В се роли обычно выступают межбанковские ставки предложения кредитных ресурсов: ЛИБОР, ПИБОР, ФИБОР и др. Надбавкой выступает фиксированная величина, являющаяся предметом договоренности сторон и, как правило, неизменная на весь срок действия кредитного договора. Размер фиксированной надбавки зависит от условий сделки и степени ее риска.
Различают также НОМИНАЛЬНУЮ и РЕАЛЬНУЮ СТАВКИ ПРОЦЕНТА. Под номинальной ставкой понимается текущая рыночная процентная ставка. Реальная ставка представляет собой номинальную ставку, скорректированную на степень инфляционного обесценения денег. Взаимосвязь между реальной (г) и номинальной (i) ставками процента впервые была представлена Дж. Фишером:
i = г + х,
где х — ожидаемый уровень инфляции.
В денежно-кредитной сфере западных стран имеется большое разнообразие процентных ставок.
Первый уровень процентных ставок — официальные процентные ставки, устанавливаемые центральными банками отдельных стран по кредитам, предоставляемым коммерческим банкам. Эти ставки носят название учетных или ставок рефинансирования.
Рефинансирование коммерческих банков может производиться либо путем прямого кредитования, либо путем переучета коммерческих векселей. Степень значимости той или иной ставки зависит от исторически сложившегося в стране развития вексельного обращения и системы рефинансирования.
Учетная ставка Центрального банка РФ, наряду с политикой в области обязательных резервов от объема привлеченных банками ресурсов и операциями на открытом рынке является одним из основных инструментов денежно-кредитного регулирования. При помощи маневриро-
===650===
вания учетным процентом Центральный банк РФ стремится регулировать объем денежной массы в обращении и темпы инфляционного обесценения денег. Так, понижение официальной учетной ставки приводит к удешевлению и увеличению предложения кредитных ресурсов на рынке. Такая политика имеет целью оживление инвестиций и стимулирование экономического роста. Проведение обратнонаправленной учетной политики ведет к сжатию денежно-кредитной массы, замедлению темпов инфляции, но одновременно это путь к сокращению объема инвестиций в экономику. Таким образом, учетная политика Центрального банка должна строиться в зависимости от состояния денежно-кредитной системы и учитывать как опасность инфляции при проводимой политике «дешевых денег», так и негативные последствия низких темпов экономического роста в периоды рестрикционной политики ЦБ РФ.
Следующий уровень процентных ставок представлен ставками предложения на межбанковском рынке кредитных ресурсов. По ставкам предложения ведущие банки осуществляют кредитование в евровалютах первоклассных банков путем размещения у последних депозитов. Примером служит ставка ЛИБОР (LIBOR) — Лондонская межбанковская ставка предложения, которая не является официально определяемой величиной, каждый крупный коммерческий банк фиксирует ее в зависимости от конъюнктуры денежно-кредитного рынка по состоянию на 11 ч утра каждого делового дня. Под ставкой ЛИБОР понимается также средняя ставка по этим банкам, рассчитываемая как средняя арифметическая.
Ставки «ПРАЙМ-РЕЙТ» — следующий уровень процентных ставок, по которым коммерческие банки предоставляют кредиты первоклассным заемщикам.
И наконец, последний уровень процентных ставок — это ставки по более рисковым ссудам предприятиям и частным лицам.
В России в настоящее время также существует целый набор процентных ставок, структура которых приближается к западной практике. Выделяются: учетная ставка Центрального банка РФ, ставки межбанковского денежного рынка, представленные большим набором инструментов (МИБИД — объявленная ставка по предоставлению кредитов коммерческими банками, МИАКР — фактическая ставка по предоставленным кредитам, рассчитываемые Информационным консорциумом как средние от ставок привлечения и размещения межбанковских кредитов, ИНСТАР — межбанковские базовые процентные ствки, рассчитываемые Межбанковским Финансовым Домом по результатам сделок, заключенных коммерческими банками), «базовые» процентные ставки по кредитованию первоклассных клиентов по обеспеченным ссудам и ставки с учетом надбавки за риск по кредитованию прочих заемщиков.
Помимо ставок кредитного рынка, рассмотренных выше, в систему процентных ставок входят ставки денежного и фондового рынков: ставки по казначейским, банковским и корпоративным векселям, проценты по государственным и корпоративным облигациям и др.
В банковской практике существуют различные методы и способы начисления процентов.
Так, в банковской практике применяются простые и сложные проценты.
===651===
Простые проценты используются прежде всего при краткосрочном кредитовании, когда один раз в квартал или другой срок, определенный договором, производится начисление процентов и выплата их кредитору. Как правило, в настоящее время преимущественно применяется изложенный выше способ. При этом общий объем платежей заемщика с учетом основной суммы долга составит:
S = P(l + ni),
где S — сумма выплат по кредиту с учетом первоначального долга;
Р — первоначальный долг;
i — ставка процентов;
п — продолжительность ссуды в годах либо отношение периода пользования ссудой в днях к применяемой базе (360 или 365 дням).
Очень часто в банковской практике приходится производить операцию, обратную процедуре начисления процентов. Это имеет место, например, в случае обращения дисконтных векселей. В этом случае при определении первоначального долга будет применяться следующая формула:

В банковской практике возможно использование сложного процента, как правило, при долгосрочном кредитовании, когда начисленные суммы не выплачиваются кредитору до окончания сделки, а увеличивают основ-
===652===
ную сумму долга. В отечественной практике метод начисления сложных процентов получил наибольшее распространение по депозитным счетам частных лиц.
При использовании этого метода размер начисленных средств включается в задолженность и на них продолжает начисляться процент. Формулу для начисления сложных процентов и определения обшей суммы задолженности можно представить в виде-

Банк должен тщательно анализировать все моменты, которые могут в конечном итоге повлиять на прибыльность банковских операций. Например, необходимо учитывать характер инфляции и в этой связи определять, что целесообразней для банка: либо наращивать сумму долга посредством начисленных, но невостребованных процентов, либо получать ежегодную плату за кредит.
Возможны различные способы начисления процента: они определяются характером измерения количества дней пользования ссудой и продолжительностью года в днях (временной базы для расчета процентов).
===653===
Так, число дней ссуды может определяться точно или приближенно, когда продолжительность любого полного месяца признается равной 30 дням. Временная база приравнивается либо к фактической продолжительности года (365 или 366 дней) или приближенно к 360 дням. Соответственно, применяют следующие варианты начисления сложных процентов:
1. Точные проценты с фактическим числом дней ссуды; этот способ дает самые точные результаты и применяется многими центральными и крупными коммерческими банками. Он характеризуется тем, что для расчета используется точное число дней ссуды, временная база равняется фактической продолжительности года. Например,
Р — сумма выданного кредита — 100 000 руб.,
i — ставка процента — 9% годовых.
К — точное число дней ссуды,
S — наращенная сумма долга.
Тогда
S = 100 000 X (1+ 0,09% X 260 дн.: 365 дн.) = 106 411 руб.
2. Обыкновенные проценты с точным числом дней ссуды. В этом случае, так же как и в предыдущем, для расчета берется точное число дней ссуды, но временная база приравнивается к 360 дням. Если срок кредита превышает 360 дней, то сумма начисленных процентов будет больше, чем предусмотрено годовой ставкой (так, если период ссуды равен 364 дням, то 364 : 360 = 1,011). Рассмотрим данный способ на предложенном выше примере:
S2 = 100 000 X (1 + 0,09% х 260 дн. : 360 дн.) = 106 499 руб.
3. Обыкновенные проценты с приближенным числом дней ссуды. Здесь продолжительность ссуды в днях определяется приближенно, временная база равна 360 дням. Считается, что точное число дней ссуды в большинстве случаев больше приближенного, поэтому и размер начисленных процентов с точным числом дней обычно больше, чем с приближенным.
В нашем примере приближенное число дней ссуды равно 257 дням (S3), учитывая это:
S3 = 100 000 х (1 + 0,09% X 257 дн.: 360 дн.) = 106 424 руб.,
Приведенные расчеты показывают, что второй способ начисления процентов, а именно обыкновенные проценты с точным числом дней ссуды дает несколько больший результат относительно двух других вариантов.
Банковская практика в России предусматривает начисление процентов по привлеченным и размещенным средствам ( за исключением долговых обязательств и операций с платежными картами) по первому способу, а именно — как точные проценты с фактическим числом дней ссуды. По векселям и депозитным сертификатам применяется способ начисления обыкновенных процентов с приближенным числом дней ссуды.
===654===
ЛИТЕРАТУРА*
- Аверьянова Л.Б. Банковская корреспонденция на английском языке: Учетно-расчетные операции. — М.: Менатеп-Ин-форм, 1996.
- Адибекое М.Г. Кредитные операции: Классификация, порядок привлечения и учет /Банк внешнеэкономической деятельности. -М.: АО «Консалт-Банкир», 1995.
- Анализ экономической деятельности клиентов банка: Учеб. пособие/ Под ред. О.И. Лаврушина. — М.: Инфра-М, 1996.
- Ачкасов А.И. Операции «А-ФОРФЭ». Общая характеристика и техника совершения / Банк внешнеэкономической деятельности. — 2-е изд. — М.: АО «Консалт-Банкир», 1994.
- Базельский комитет по банковскому надзору: Сборник документов и материалов / Сост. Ю. В. Кузнец. -М-: Центр подготовки персонала ЦБ РФ, 1997.
- Банки и банковские операции: Учебник / Под ред. Е.Ф.Жукова. -М.: Банки и биржи, ЮНИТИ, 1997.
- Банки на развивающихся рынках: В 2 т.: Пер. с англ. Т. 1. Укрепление руководства и повышение чувствительности к переменам / Д. МакНотон, Д. Дж. Карлсон, К.Т, Дитц и др. — М.: Финансы и статистика, 1994.
- Банки на развивающихся рынках: В 2 т.: Пер. с англ. Т. 2. Интерпретирование финансовой отчетности /К. Дж. Барлтроп, Д. МакНотон. — М.: Финансы и статистика, 1994.
- Банковские операции: Учетно-ссудные операции и агентские услуги банков: Учеб. пособие. -Ч. 2/Под ред. О. И. Лаврушина, -М.: Инфра-М, 1996.
- Банковское дело и финансирование инвестиций. В 2 т. Пер. с англ. / Под ред. Н. Брука, Институт экономического развития Всемирного банка, 1995.
- Белых Л.П. Устойчивость коммерческих банков: Как банкам избежать банкротства. -М.: Банки. ЮНИТИ, 1996.
+++* Список литературы подготовлен канд. экон. наук, доц. Л .А. Гуриной и канд. экон. наук И.Е. Шакер.
===655===
- Беляев С. Г. Русско-французские банковские группы в период экономического подъема 1909-1914 гг. — СПб: АО «ЭН-ПИ», 1995.
- Березина М.П. Безналичные расчеты в экономике России. Анализ практики. — М.: АО «Консалт-Банкир», 1997.
- Букато В. И., Львов Ю.И. Банки и банковские операции в России /Под ред. М.Х. Лапидуса. — М.: Финансы и статистика, 1996.
- Блумфшъд А. Как взять кредит в банке. — М.: Инфра-М, 1996.
- Введение в банковское дело. Пер. с нем. / Кол. авторов под рук. Гюнтера Асхауэра. — М.: ИПФ «Мир и культура», 1997.
- Гончаренко Л.И. Налогообложение коммерческих банков: Учеб. пособие / Под ред. Л.П. Павловой. — М.: Финансы и статистика, 1997.
- Голубович А.Д. и др. Валютные операции в коммерческих банках. -М.: Менатеп-Информ, 1994.
- Горина С.А. Учет в банке на основе нового плана счетов. Проверка правильности отражения банковских операций. — М.: Приор, 1998.
- Гарантии и аккредитивы в современной банковской практике: Учебник для Высших финансовых школ и колледжей / Под ред. А.Д. Голубовича. -М.: Менатеп-Информ, 1994.
- Гавалъда Кристиан Стуфле Жан. Банковское правой Учреждение — Счета — Операции — Услуги: Пер. с фр. /Под ред. В.Я. Лисняка. — М.: Финстатинформ, 1996.
- Денежная реформа в посткоммунистических странах: Пер. с англ. / Под ред. Дж. Дорна, P.M. Нуреева. — М.: Catallaxy, 1995.
- Гроссман Репе Клаус. Как вести дела с банками: Кредиты, денежные вклады, платежный оборот: Пер. с нем. — М.: Международные отношения, 1996.
- Ермаков С. Л. Работа коммерческого банка по кредитованию заемщиков: Методические рекомендации. — М.: Компания «Алее», 1995.
===656===
- Закон Российской Федерации «О внесении изменений и дополнений в Закон РСФСР «О банках и банковской деятельности в РСФСР» от 3 февраля 1996 г. // Деньги и кредит. -1996. —
- №2.
- Закон Российской Федерации «О внесении изменений и дополнений в Закон РСФСР «О Центральном банке РСФСР (Банке России)» от 26 апреля 1995 г. // Деньги и кредит. — 1995. -№ 5; Экономика и жизнь. — 1995. — № 19.
- Закон Российской Федерации «О денежной системе Российской Федерации» от 23 сентября 1992 г.// Ведомости съезда народных депутатов РСФСР и Верховного Совета РСФСР. -1992. -№43.
- ЗамиусскаяЕ.Р., КочмолаКВ., Лазарева Н.А., Чубарова Г.П. Внутренний аудит банка. — М.: «Экспертное бюро», 1997.
- Европейский банк реконструкции и развития и другие финансовые учреждения. Европейская валютная система. Европейский валютный союз: Учеб. пособие на немецком языке / Сост. И. Н. Шахнес. — М.: ЦПП ЦБ РФ, 1996.
- Иванов В.В. Как надежно и выгодно вкладывать деньги в коммерческие банки: Надежность банка. — М.: Инфра-М, 1996.
- Иванов В.В. Анализ надежности банка. — М.: Русская Деловая Литература, 1996.
- Кириллов И.А. Ломбарды в России. — М.: СО «АННИЯ», 1992.
- Козлова Е.П., Галапииа Е.Н. Бухгалтерский учет в коммерческих банках. — М.: Финансы и статистика, 1996.
- Комментарии к Базовым принципам эффективного надзора за банковской деятельностью. Подготовлены Базельским комитетом по банковскому регулированию в апреле 1997 г. Утверждены письмом АРБ от 24 июня 1997 г. № А-02/1-472// Вестник АРБ. -1997. — № 20; Бизнес и банки. — 1997. — № 32.
- Комионский С.А. Наука и искусство управления современным банком. — М.: InterstaTO Publishers, 1995 (Мое. ин-т экономики, политики и права).
- Коровкин В.В., Кузнецова Г.В. Оформление валютных операций. -М.: Приор, 1995.
- Кочоеич Е. Финансовая математика: теория и практика финансово-банковских расчетов: Пер. с серб. — М.: Финансы и статистика, 1994.
===657===
- Макарова Г. П. Система банковского маркетинга: Учеб. пособие. -М.: Финстатинформ, 1997.
- Масленченков Ю. С. Финансовый менеджмент в коммерческом банке. — Кн. 1. Фундаментальный анализ. — М.: Перспектива, 1996.
- Масленченков Ю. С. Финансовый менеджмент в коммерческом банке. — Кн. 2. Технологический уклад кредитования. — М: Перспектива, 1996.
- Масленченков Ю. С. Финансовый менеджмент в коммерческом банке. — Кн. 3. Технология финансового менеджмента клиента. — М: Перспектива, 1997.
- Межбанковский Финансовый Дом: Рассказ о компании. -М., 1996.
- Международные валютно-кредитные и финансовые отношения: Учебник /Под ред. Л.Н. Красавиной. — М.: Финансы и статистика, 1994.
- МиркипЯ. М. Банковские операции. Ч. 3: Инвестиционные операции банков. Эмиссионно-учредительская деятельность банков. -М.: Инфра-М, 1996.
- Молчанов А.В. Коммерческий банк в современной России: Теория и практика. — М.: Финансы и статистика, 1996.
- Московкина Л.А. Кредитно-банковская система Южной Кореи. — М: ЦПП ЦБ РФ, 1996.
- Нидеккер Г. Л. и др. Анализ эффективности валютно-обменных операций банка. — М.: Русская Деловая Литература, 1996.
- Нестерова Т. Н. Банковские операции. Ч. 4: Банковское обслуживание внешнеэкономической деятельности: Учеб. пособие. — М.: Инфра-М, 1996.
- Об утверждении Правил ведения бухгалтерского учета в кредитных организациях, расположенных на территории Российской Федерации и дополнений и изменений к Плану счетов бухгалтерского учета в кредитных организациях Российской Федерации. Приказ ЦБ РФ от 18 июня 1997 г. № 02-263//Вестник Банка России. — 1997. — № 49.
- Операционная работа в коммерческих банках: Сборник нормативных документов /Сост. Г.А. Яковлев. — М.: Менатеп-Информ, 1996.
===658===
- Панова Г. С. Анализ финансового состояния коммерческого банка. — М.: Финансы и статистика, 1996.
- Панова Г. С. Кредитная политика коммерческого банка. -М.: МКЦ Дис, 1997.
- Поляков В.П., МосковкинаЛ.А. Основы денежного обращения и кредита: Учеб. пособие. — М.: Инфра-М, 1995.
- Поляков В.П., МосковкипаЛ. А. Структура и функции центральных банков. Зарубежный опыт: Учеб. пособие-М.: Инфра-М, 1996.
- Полфреман Дэвид Форд Филип. Основы банковского дела. Пер. с англ. М.: Инфра-М, 1996.
- Рассказов Е. А. Управление свободными ресурсами банка. -М.: Финансы и статистика, 1996.
- Роуз Питер С. Банковский менеджмент. Предоставление финансовых услуг. Пер. с англ. — М.: Дело, 1997.
- Руководство по кредитному менеджменту: Пер. с англ. / Под ред. В.Эдвардса. — М., 1996.
- Сидельникова Д. Б. Аудит коммерческого банка. — М.: Буквица, 1996.
- Симоновский А. Ю. Финансово-банковский сектор российской экономики: Вопросы формирования и функционирования. — М.: Соминтэк, 1995.
- Соколинская Н. Э. Учет и анализ краткосрочных и долгосрочных кредитов. — М.: АО «Консалт-Банкир», 1997.
- Тагирбеков К. Р, Опыт развития технологии управления коммерческим банком. — М.: Финансы и статистика, 1996.
- Сеферова Н. А., Можаева Н. Г. Методические указания по теме «Договоры, используемые для осуществления банковских операций. Типовые формы». — М.: ФА, 1996.
- Смит Вера. Происхождение центральных банков: Пер. с англ.-М.: Институт Национальной Модели Экономики, 1996.
- Усоскин В. М. Современный коммерческий банк: Управление и операции. — М., 1994.
===659===
- Уткин Э.А. Стратегический менеджмент: Способы выживания российских банков. — М.: Фонд Экономического Просвещения, 1996.
- Уайтииг Д. П. Осваиваем банковское дело: Пер. с англ. / Под ред. В.В.Мирюкова. -М.: Банки и биржи, ЮНИТИ, 1996.
- Финансовая академия при Правительстве Российской Федерации. Нововведения в банковском бизнесе России: Сб. науч. трудов /Отв. ред. Э.А.Уткин. — М.: ФА, 1996.
- Ширинская Е, Б. Операции коммерческих банков: российский и зарубежный опыт. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 1995.
- Ширинская 3. Г., Нестерова Т. Н., Соколипская Н. Э. Бухгалтерский учет и операционная техника в банках. — М., 1997.
- Экономический анализ деятельности банка: Учеб. пособие. -М.: Инфра-М, 1996.
===660===
Предисловие.. 3
Раздел I. ХАРАКТЕРИСТИКА БАНКА КАК ПРЕДПРИЯТИЯ.7
Глава 1. Сущность банка и организационные основы его построения….9
1.1. Представление о сущности банка с позиции его исторического развития…9
1.2. Современные представления о сущности банка.14
1.3. Банк как элемент банковской системы…18
1.4. Организационные основы построения аппарата управления банком…24
1.5. Структура аппарата управления банка и задачи его основных подразделений….28
Глава 2 Правовые основы банковской деятельности….34
2.1. Структура современного банковского законодательства..34
2.2. Эволюция банковского законодательства в России…37
2.3. Особенности первых банковских законов 1990 г….38
2.4. Основная характеристика современного банковского законодательства….41
2.5. Законодательные основы деятельности современного банка..44
2.6. Обеспечение безопасности банков…… 54
2.7. Банковская монополия..62
2.8. Взаимоотношения банка с клиентами..63
===661===
Раздел II ОБЩИЕ ВОПРОСЫ ДЕЯТЕЛЬНОСТИ КОММЕРЧЕСКОГО БАНКА….67
Глава 3 Ресурсы коммерческого банка и его капитальная база…69
3.1. Ресурсы коммерческого банка: их структура и характеристика…69
3.2. Понятие и структура собственного капитала банка..70
3.3. Оценка достаточности собственного капитала банка…75
3.4. Привлеченные средства коммерческого банка…86
Глава 4 Структура и качество активов банка….94
4.1. Состав и структура активов.94
4.2. Качество активов банка..101
Глава 5 Доходы и прибыль коммерческого банка….115
5.1. Доходы коммерческого банка….115
5.2. Расходы коммерческого банка…119
5.3. Процентная маржа…121
5.4. Оценка уровня доходов и расходов коммерческого банка….125
5.5. Формирование и использование прибыли коммерческого банка..128
5.6. Оценка уровня прибыли коммерческого банка….130
Глава 6 Ликвидность и платежеспособность коммерческого банка…140
6.1. Понятие и факторы, определяющие ликвидность и платежеспособность коммерческого банка…140
6.2. Российская практика оценки ликвидности коммерческих банков..146
6.3. Зарубежный опыт оценки ликвидности коммерческих банков..163
662Глава 7 Банковская отчетность……159
7.1. Значение и виды банковской отчетности…169
7.2. Баланс банка и принципы его построения….170
7.3. Текущая бухгалтерская отчетность….202
7.4. Годовая бухгалтерская отчетность.204
7.5. Проблемы перехода на международные принципы учета в банках..205
Раздел III УСЛУГИ И ОПЕРАЦИИ КОММЕРЧЕСКОГО БАНКА….211
Глава 8 Пассивные операции банков.213
8.1. Структура и общая характеристика пассивных операций банков.213
8.2. Депозитные и внедепозитные операции..214
Глава 9 Система оценки кредитоспособности клиентов банка..,…222
9.1. Понятие и критерии кредитоспособности клиента…222
9.2. Кредитоспособность крупных и средних предприятий.224
9.2.1. Финансовые коэффициенты оценки кредитоспособности клиентов коммерческого банка.224
9.2.2. Анализ денежного потока как способ оценки кредитоспособности заемщика .232
9.2.3. Анализ делового риска как способ оценки кредитоспособности клиента 235
9.2.4. Определение класса кредитоспособности клиента..237
9.3. Оценка кредитоспособности мелких предприятий…240
9.4. Оценка кредитоспособности физического лица….241
===663===
Глава 10 Кредитование юридических лиц..243
10.1. Фундаментальные элементы системы кредитования…243
10.2. Субъекты кредитования и виды кредитов.245
10.3. Объекты кредитования….249
10.4. Особенности современной системы кредитования….251
10.5. Условия кредитования.252
10.6. Этапы кредитования….254
10.7. Общие организационно-экономические основы кредитования…256
10.7.1. Методы кредитования и формы ссудных счетов.257
10.7.2. Кредитная документация, представляемая банку на начальном и последующих этапах кредитования…259
10.7.3. Процедура выдачи кредита.262
10.7.4. Порядок погашения ссуды…264
Глава 11 Организация отдельных видов кредита..269
11.1. Современные способы кредитования.269
11.2. Кредит по овердрафту и контокорренту….270
11.3. Ипотечный кредит…273
11.4. Организация потребительского кредита (кредитование физических лиц).283
11.5. Межбанковские кредиты.295
11 .6. Кредиты Банка России…304
11.7. Консорциальные (синдицированные) кредиты….315
===664===
Глава 12 Содержание кредитного договора банка с клиентом..320
12.1. Правовой и экономический аспекты кредитного договора банка с клиентом.320
12.2. Основные требования к содержанию и форме кредитного договора..323
12.3. Международный опыт использования кредитных договоров в банковской практике.329
12.4. Анализ и оценка российской практики составления кредитных договоров банка с клиентом…334
Глава 13 Формы обеспечения возвратности кредита.337
13.1. Понятие формы обеспечения возвратности кредита..337
13.2. Залог и залоговый механизм…339
13.3. Уступка требований (цессия) и передача права собственности….,.351
13.4. Гарантии и поручительства….354
13.5. Классификация предприятий по степени кредитного риска в зависимости от финансового состояния и качества обеспечения кредита.,…359
Глава 14 Организация платежного оборота и межбанковские корреспондентские отношения.363
14.1. Основы платежного оборота..363
14.2. Платежная система и ее элементы..366
14.3. Принципы организации безналичных расчетов….373
14.4. Расчеты в нефинансовом секторе (в народном хозяйстве)…377
14.5. Расчеты в финансовом секторе (между банками).. 407
===665===
Глава 15 Лизинговые операции коммерческих банков..455
15.1. История возникновения и развития лизинга.455
15.2. Сущность лизинговой сделки..459
15.3. Основные элементы лизинговой операции….460
15.4. Классификация видов лизинга и лизинговых операций..466
15.5. Организация и техника лизинговых операций…..472
15.6. Содержание лизингового договора….473
15.7. Риски лизинговых сделок….476
Глава 16 Операции коммерческих банков с ценными бумагами..478
16.1. Виды банковской деятельности на рынке ценных бумаг…478
16.2. Выпуск банком собственных ценных бумаг..480
16.3. Инвестиционные операции коммерческих банков с ценными бумагами…490
16.4. Операции репо..494
Глава 17 Валютные операции коммерческих банков……497
17 Л. Регулирование валютных операций коммерческих банков..497
17.2. Экономические основы валютных операций коммерческих банков России.505
17.3. Классификация и понятие валютных операций коммерческих банков России .512
17.4. Валютные риски и методы их регулирования..530
17.5. Финансовые инструменты как метод страхования валютных рисков…563
===666===
Глава 18 Прочие операции коммерческих банков..584
18.1. Классификация и общая характеристика прочих операций коммерческих банков….584
18.2. Правовые основы развития прочих операций коммерческих банков..585
18.3. Организация прочих операций коммерческих банков.586
Глава 19 Новые банковские продукты и услуги….604
19.1. Пластиковые карты. Особенности применения пластиковых карт в российской и зарубежной практике …. 604
19.2. Банкомат как элемент электронной системы платежей…626
19.3. Межбанковские электронные переводы денежных средств в торговых организациях..627
19.4. «Home banking» — банковское обслуживание клиентов на дому и на их рабочем месте…629
19.5. Хранение ценностей.. 632
19.6. Форфейтинговые операции банков…632
19.7. Опционы, фьючерсы, свопы….635
Глава 20 Банковский процент и процентные начисления..638
20.1. Банковский процент и механизм его использования….638
20.2. Процентный риск, методы его оценки и управления….643
20.3. Процентные ставки и методы начисления процентов…650
Литература
Банковское дело: Учебник . — 2-е изд., перераб. и доп./ Под ред. Б23 О.И. Лаврушина. — М.: Финансы и. статистика, 2005. — 672 с: ил. ISBN 5-279-02102-4
Настоящее издание учебника подготовлено преподавателями Финансовой академии при Правительстве РФ по специальностям «Финансы икредит» и «Бухгалтерский учет, анализ и аудит». Рассматриваются теория и практика работы банка, правовые и экономические основы его деятельности. Наибольшее внимание уделено организации и порядку оформления отдельных банковских операций, технологии банковского дела. Приводятся конкретные расчеты, производимые банком в процессе выполнения своих функций (1-еизд. — 1998г).
Для студентов и преподавателей экономических вузов и факультетов, работников банков.
Учебник
Лаврушин Олег Иванович
Мамонова Ината Дмитриевна
Валенцева Наталья Игоревна и др.
БАНКОВСКОЕ ДЕЛО
Заведующая редакцией Н.Ф. Карпычева Редактор В.М. Щербакова Младший редактор Г.В. Серебрякова Художественный редактор ОМ. Поленова Технический редактор Т.С. Маршина Корректоры Т.М. Колпакова, Т.М. Васильева Компьютерный набор О.В. Фортунатовой, Т.Н. Помадчиной Компьютерная верстка Е.Ф. Тимохиной
Оформление художника Н.М.Биксептеева
Подписано в печать 08.12.2004. Формат 70×100/16 Гарнитура «Тайме». Печать офсетная Усл.п.л.54,6. Уч.-изд. л. 48,31 Тираж 5000 экз. Заказ зово «с» 002
Издательство «Финансы и статистика» Москва, ул. Покровка, 7 Телефон (095) 925-35-02, факс (095) 925-09-57 E-mail: mail@finstat.ru http://www.finstat.ru
ОАО «Типография «Новости» 105005, Москва, ул.Ф.Энгельса, 46
Отличие простых процентов от сложных
Несомненно, выгодность банковского вклада, в первую очередь, определяет процентная ставка. Ведь именно на нее ориентируется каждый потенциальный клиент. Но, на самом деле, вкладчику нужно, в частности, обратить внимание не на годовую процентную ставку, а на метод начисления прибыли. Ведь в финансовой системе банка существуют два понятия: простой и сложный процент. А для каждого вкладчика нужно точно знать, что такое простые и сложные проценты понятие и формулы, чтобы определить, какой вклад будет наиболее выгодный для него.

Что такое простой процент
В первую очередь, простой процент – это начисление вознаграждения за размещение вклада на банковском счете за весь период хранения средств. Если говорить простыми словами, то простой процент начисляется лишь по окончании срока действия депозитного договора, он определяется в годовой процентной ставке. Причем, если договор автоматически продлевается на следующий срок, то вознаграждение за предыдущий период не причисляется к телу депозита.
Чтобы максимально точно понять, что такое простая система начисления прибыли рассмотрим пример. Вы разместили в банке 50000 рублей под 7% годовых на один год. По окончании срока действия договора ваша прибыль составит 50000×0,07=3500 рублей. При автоматической пролонгации договора на следующий срок ваша прибыль составит снова 3500 рублей. То есть спустя 2 года вы сможете в банке получить 50000+3500+3500=57000 рублей.
Важно! Формула расчета простых процентов выглядит следующим образом: K=D×p. Где K – сумма прибыли, D – тело депозита, p – годовая процентная ставка (в формуле нужно указывать не годовую ставку, а ставку, деленную на 100).
Если вы размещаете средства на срок меньше чем на один год, то соответственно процентная ставка годовая делится на 12 и умножается на количество месяцев, в течение которых средства были на банковском счете. Например, если срок депозита 3 месяца, а процентная ставка 10% в год, то общая прибыль рассчитывается следующим образом.0,1/12×3=0,025. Например, если вы разместили 50000 рублей сроком на 3 месяца, то прибыль по окончании срока действия договора будет следующий: 50000×0,025=1250 рублей.

Формулы простых и сложных процентов
Сложные проценты по вкладу
Отличие простых процентов от сложных на самом деле довольно большое. При выборе депозитного продукта наверняка каждому приходилось слышать о таком понятии, как капитализация. То есть это та схема начисления прибыли, при которой начисленная прибыль причисляется к телу депозита, а на него в будущем снова начисляется доход.
Обратите внимание, что капитализация осуществляется с определенной периодичностью, например, один раз в неделю, в месяц в квартал или год.
Отсюда можно сделать вывод, что капитализация позволяет получить большую прибыль по сравнению с простым процентом. Чтобы наглядно в этом убедиться рассмотрим формулу расчета сложных процентов, а выглядеть она будет следующим образом: B=(K×H×P/N)/100, где:
- B – размер начисленной прибыли;
- K – тело депозита;
- H – годовая ставка;
- P – количество дней, в течение которых происходит капитализация;
- N – число дней в году.
Чтобы наглядно понять, как именно будет рассчитываться сложный процент. Рассмотрим простой пример. Сумма депозита 50000 рублей процентная ставка в год 7%, капитализация осуществляется ежемесячно, срок действия договора один год. Произведем расчет прибыли за первый месяц пользования депозитом: B=(50000×7×30/365)/100=287,6 рублей – это прибыль за первый месяц. В следующем периоде расчет будет выглядеть следующим образом: B=(50287,6×7×31/365)/100=298,9 рублей.
Из вышеприведенного примера можно сделать вывод, что капитализация позволяет получать с каждым месяцем большую прибыль по сравнению с предыдущим. Вот только при выборе депозитного предложения обязательно обратить внимание, с какой периодичностью осуществляется капитализация процентов, чем чаще, тем больше выгоды получает клиент.
В чем отличие
На самом деле система начисления процентов по вкладам сильно различается в первую очередь по той причине, что с капитализацией процентов выгода депозита может быть значительно выше, нежели при простой системе. Потому что при простой системе прибыль растет в арифметической прогрессии, а при сложной в геометрической. Чтобы наглядно в этом убедиться, ниже приведена схема сложных процентов в сравнении со схемой простых процентов.

Схема сложных процентов в сравнении со схемой простых процентов
Но, в этом вопросе также есть подводные камни. Условия банковских вкладов строго индивидуальны, поэтому при выборе депозитного продукта в первую очередь обратите внимание на количество периодов капитализации за весь срок действия договора. Например, банк указывает, что по вашему депозитному договору предусмотрена капитализация процентов, но она осуществляется 1 раз в 6 месяцев, то есть первый доход, вы получите спустя полгода после заключения соглашения с банком. При этом вы решили разместить средства лишь на 3 месяца, соответственно, вы получите свои средства раньше, чем банк проведет капитализацию процентов и в данном случае целесообразней выбрать простой расчет процент по вкладу.
Важно! Большинство банков предлагают по одному и тому же депозитному предложению своим клиентам сделать выбор получать прибыль с определенной периодичностью или причислять себя к телу депозита, соответственно, у клиента есть возможность выбрать по какой системе простой или сложной, он хотел бы получать свой доход.
На самом деле понять, в чем состоит принципиальная разница между простыми и сложными процентами достаточно просто, но все же нюанс заключается в том, что банки в договоре не указывают такие понятия, как простые и сложные проценты каждый потенциальный вкладчик должен обращать внимание на все условия договора. Если в договоре указано, что проценты выплачиваются по окончании срока действия договора, соответственно, капитализация по такому договору не предусмотрена.
Простые и сложные проценты — что это такое? Калькулятор сложных процентов от Вебинвеста
Начисление процентов — одна из основных операций в экономике и инвестировании. Самый близкий всем пример — депозит в банке, где вложенные деньги в конце периода возвращаются к владельцу с прибылью.
А что будет, если повторить этот цикл несколько раз? Тут то и появляется понятие простых и сложных процентов, которым посвящена эта статья.
Простые и сложные проценты
Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.
Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.
Простой процент — прибыль по многоразовым вкладам за каждый период времени всегда начисляется только на первоначальную сумму.
Пример: депозит 5000$ под 20% годовых. По схеме простого процента и в первый, и во второй, и в любой другой год прибыль составит 1000$. Чтобы узнать прибыль за N лет, просто умножьте прибыль за один год на число N.
Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты по многоразовым вкладам за каждый период начисляются на первоначальную сумму и всю полученную до этого прибыль.
Пример: депозит 5000$ под 20% годовых. В первый год прибыль составит 5000$ * 20% = 1000$, во второй (5000$ + 1000$) * 20% = 1200$, в третий (5000$ +1000$ + 1200$) * 20% = 1440$ и так далее.
Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.
В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.
Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:
Простые и сложные проценты на одном графике
Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.
К СОДЕРЖАНИЮ
Формулы сложных процентов по вкладам и примеры решения задач
Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:
- начальная сумма вклада (K нулевая или К0)
- ставка доходности (R) — переводится из процентов в число (10% = 0.1)
- количество периодов реинвестирования, то есть лет (n)
А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:
Конечная сумма при расчёте сложных процентов по вкладу
Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?
Для начала, давайте узнаем конечную сумму вклада по формуле:
K = 10000$ * (1 + 0.1)5 = 16105.1$
Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:
P = K — К0 = 16105.1$ — 10000$ = 6105.1$
Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:
P (%) = K/К0 — 1 = 16105.1$ / 10000$ — 1= 61.05%
Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:
Формула расчёта сложных процентов для поиска стартовой суммы вклада
Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером.
Используем формулу:
К0 = 1000000₽ / (1 + 0.2)3 = 578703.7₽
Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.
Начнем с процентной ставки:
Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки
Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.
Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:
K = К0 + P = 20000$ + 10000$ = 30000$
А теперь можно использовать формулу:
R = (30000$ / 20000$) ^ 1/3 — 1 = 14.47%
Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.
Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:
Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования
Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?
Подставляем в формулу:
n = log1+0.25 100000/50000 = 3.11 лет
Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.
Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.
Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?
Чтобы узнать результат, нужно создать табличку:
Расчёт результатов инвестирования с доливками, с учётом сложных процентов
В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…
Разумеется, считать эти таблички каждый раз — довольно напряжно, решать логарифмы — тем более. Поэтому специально для вас при помощи программы Microsoft Excel я сделал небольшой файлик для решения задач по сложным процентам.
К СОДЕРЖАНИЮ
Калькулятор сложных процентов от Вебинвеста
Многие формулы сложных процентов в математике на обычном калькуляторе не посчитаешь — нужно использовать специальные программы или сайты. Microsoft Excel позволяет делать практически любые прикладные расчёты быстро и удобно — всего-то нужно скачать файл и работать с ним.
По формулам из статьи я сделал небольшой калькулятор для расчёта сложных процентов. Вот так выглядит одна из страниц:
Скриншот из калькулятора сложных процентов с капитализацией.
С помощью файла вы сможете решить задачи, которые мы рассматривали по ходу статьи:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт нужной процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом добавочных вложений или снятия прибыли.
Как получить калькулятор сложных процентов от Вебинвеста? Очень легко — воспользуйтесь формой ниже:
Больше подробностей о калькуляторе сложных процентов вы можете узнать на этой странице.
К СОДЕРЖАНИЮ
Ну что, ощутили магию сложных процентов? Если да, поделитесь статьёй в соцсетях, пусть ваши друзья тоже её почувствуют 🙂
Удачи и терпения в инвестициях!
Александр Дюбченко (добавляйтесь в друзья Вконтакте и на Facebook). С 2016 года веду блог об инвестировании в Интернете, изучаю инвестиции в ПАММ-счета, акции, криптовалюты, драгоценные металлы, валютный рынок. Также разрабатываю вспомогательные инструменты для инвесторов на основе MS Excel. Всегда готов ответить на любые ваши вопросы.
Понятие простого и сложного процента
Предоставляя денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является 1 год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления:
• схема простых процентов (simple interest);
• схема сложных процентов (compound interest).
Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р; требуемая доходность — г (в долях единицы). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Pr. Таким образом, размер инвестированного капитала (Rn) через п лет будет равен:
Rn = Р + Р r + … + Рr = Р* (1 + n r). (3)
Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с обшей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:
к концу первого года: FV1 = Р + Рr = Р(1+ r);
к концу второго года: FV2= FV1 + FV1r = FV1 *(1 + г) = P * (1+ r)2;
к концу n-го года: FVn = P*(1+r)n
Как же соотносятся величины Rn и Fn. Это чрезвычайно важно знать при проведении финансовых операций. Все зависит от величины п
Графически взаимосвязь можно представить следующим образом (рис. 2).

Рис.2 Простая и сложные схемы наращения капиталаТаким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:
• более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);
• более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);
• обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.
В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя п берется величина, характеризующая удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округляться: месяц — 30 дней; квартал — 90 дней; полугодие — 180 дней; год — 360 (или 365,366) дней.
Пример
Рассчитать наращенную сумму с исходной суммы в 1 тыс. руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20%; б) периоды наращения: 90 дней, 180 дней, 1 год, 5 лет, 10 лет (если считать, что в году 360 дней).
Результаты расчетов имеют следующий вид:(тыс.руб.)
| Схема начисления | 90 дней (n=1/4) | 180 дней (n=1/2) | 1 год (n=1) | 5 лет (n=5) | 10 лет (n=10) |
| Простые проценты Сложные проценты | 1.05 1.0466 | 1.10 1.0954 | 1.20 1.20 | 2.0 2.4883 | 3.0 6.1917 |
Таким образом, если денежные средства размещены в банке на срок в 90 дней (менее одного года), то наращенная сумма составит: при использовании схемы простых процентов — 1,05 тыс. руб.; при использовании схемы сложных процентов — 1,0466 тыс. руб. Следовательно, более выгодна первая схема (разница — 3,4 руб.). Если срок размещения денежных средств превышает один год, ситуация меняется диаметрально — более выгодна схема сложных процентов, причем наращение в этом случае идет очень быстрыми темпами. Так, при ставке 20% годовых удвоение исходной суммы происходит следующим темпом; при использовании схемы простых процентов—за пять лет, а при использовании схемы сложных процентов — менее чем за четыре года.
Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.
Формула сложных процентов является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя FM1(r, n), называемого мультиплицирующим множителем для единичного платежа, обеспечивающего наращение стоимости, табулированы для различных значений r и n (см. приложение 3).
Формула наращения по схеме сложных процентов имеет вид:
FVn=P(1+r)n= P FM 1 (r, n), где
FVn –сумма, ожидаемая к поступлению через п базисных периодов;
r – ставка наращивания
FM 1 (r, n),- мультиплицирующий множитель.
Множитель FM1 (r,n)= (1+r)n
Экономический смысл множителя FM1(r, п) состоит в следующем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т.п.) через п периодов при заданной процентной ставке r, т.е. он оценивает будущую стоимость одной денежной единицы. Подчеркнем, что при пользовании этой и последующими финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки. Так, если базисным периодом начисления процентов является квартал, то в расчетах должна использоваться квартальная ставка.
3.3.2. ОБЛАСТИ ПРИМЕНЕНИЯ СХЕМЫ ПРОСТЫХ ПРОЦЕНТОВ
На практике многие финансовые операции выполняются в рамках одного года, при этом могут использоваться различные схемы и методы начисления процентов. В частности, большое распространение имеют краткосрочные ссуды, т.е. ссуды, предоставляемые на срок до одного года с однократным начислением процентов. Как отмечалось выше, в этом случае для кредитора, диктующего чаще всего условия финансового контракта, более выгодна схема простых процентов, при этом в расчетах используют промежуточную процентную ставку, которая равна доле годовой ставки, пропорциональной доле временного интервала в году.
F = P*(1+f*r)(7.5)
где r— годовая процентная ставка в долях единицы;
t— продолжительность финансовой операции в днях;
T — количество дней в году;
f — относительная длина периода до погашения ссуды.
Для наглядности формулу (7.5) можно записать следующим образом:
F = P* (1+t*r/T), т.е. дробь r/Т представляет собой дневную ставку, а произведение t * r/Т— ставку за t дней.
Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день. В зависимости от того, чему берется равной продолжительность (года, квартала, месяца), размер промежуточной процентной ставки может быть различным. Возможны два варианта:
• точный процент, определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);
• обыкновенный процент, определяемый исходя из приближенного числа дней в году, квартале и месяце (соответственно 360, 90, 30).
При определении продолжительности периода, на который выдана ссуда, также возможны два варианта:
• принимается в расчет точное число дней ссуды (расчет ведется по дням);
• принимается в расчет приблизительное число дней ссуды (исходя из продолжительности месяца в 30 дней).
Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами (одна для обычного года, вторая для високосного), в которых все дни в году последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня (приложение 2).
3.3.3. ВНУТРИГОДОВЫЕ ПРОЦЕНТНЫЕ НАЧИСЛЕНИЯ
В практике выплаты дивидендов нередко оговаривается величина годового процента и количество периодов начисления процентов. В этом случае расчет ведется по формуле сложных процентов по подинтервалам и по ставке, равной пропорциональной доле исходной годовой ставки по формуле
Fn=P*(1+r/m)n*m, где г — объявленная годовая ставка; m — количество начислений в году; n — количество лет.
Пример
Вложены деньги в банк в сумме 5 тыс. руб. на два года с полугодовым начислением процентов под 20% годовых. В этом случае начисление процентов производится четыре раза по ставке 10% (20% : 2), а схема возрастания капитала будет иметь вид:
Период Сумма, с которой идет Ставка Сумма к концу
начисление (в долях ед.) периода
6 месяцев 5,0 х 1,10 = 5,5
12 месяцев 5,5 х 1,10 = 6,05
18 месяцев 6,05 х 1,10 = 6,655
24 месяца 6,655 х 1,10 = 7,3205
Если пользоваться формулой (7.7), то m = 2, п = 2, следовательно: Fn = 5 * (1 + 20% : 100% : 2)4= 7,3205 тыс. руб.
Пример
В условиях предыдущего примера проанализировать, изменится ли величина капитала к концу двухлетнего периода, если бы проценты начислялись ежеквартально.
В этом случае начисление будет производиться восемь раз по ставке 5% (20% : 4), а сумма к концу двухлетнего периода составит:
Fn = 5 * (1 + 0,2/4)8 = 7,387 тыс. руб.
Таким образом, можно сделать несколько простых практических выводов:
при начислении процентов: 12% годовых не эквивалентны 1% в месяц (эта ошибка очень распространена среди начинающих бизнесменов);
чем чаще идет начисление по схеме сложных процентов, тем больше итоговая накопленная сумма.
Заметим, что для простых процентов такие выводы не имеют место. Одно из характерных свойств наращения по простым процентам заключается в том, что наращенная сумма не изменяется с увеличением частоты начислений простых процентов. Например, наращение Простыми процентами ежегодно по ставке 10% годовых дает тот же результат, что и ежеквартальное наращение простыми процентами по ставке 2,5% за квартал. При наращении по сложным процентам ежеквартальное начисление составляет больший результат, чем ежегодное.
3.3.4. НАЧИСЛЕНИЕ ПРОЦЕНТОВ ЗА ДРОБНОЕ ЧИСЛО ЛЕТ
Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:
• по схеме сложных процентов:
Fn=P∙(l +r)w+f (7.8)
• по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов — для дробной части года):
Fn=P∙(1+r)w∙(1+f∙r) (7.9)
гае w — целое число лет; /— дробная часть года.
Пример
Банк предоставил ссуду в размере 10 тыс. руб. на 30 месяцев под 30% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
По формуле (7.8): Fn = 10 • (1 + 0,3)2+0-5 = 19,269 тыс. руб.
По формуле (7.9): Fn = 10 • (1 + 0,3)2• (1 + 0,3 ∙ 0,5) =19,435 тыс. руб.
Таким образом, в условиях задачи смешанная схема начисления процентов более выгодна для банка.
3.3.5. ЭФФЕКТИВНАЯ ГОДОВАЯ ПРОЦЕНТНАЯ СТАВКА
Различными видами финансовых контрактов могут предусматриваться различные схемы начисления процентов. Как правило, в этих контрактах оговаривается номинальная процентная ставка, обычно годовая. Эта ставка, во-первых, не отражает реальной эффективности сделки и, во-вторых, не может быть использована для сопоставлений. Для того чтобы обеспечить сравнительный анализ эффективности таких контрактов, необходимо выбрать некий показатель, который был бы универсальным для любой схемы начисления. Таким показателем является эффективная годовая процентная ставка ге, обеспечивающая переход от Р к Fn при заданных значениях этих показателей и однократном начислении процентов.
Общая постановка задачи может быть сформулирована следующим образом. Задана исходная сумма Р, годовая процентная ставка (номинальная) r, число начислений сложных процентов m. Этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной величины F1. Требуется найти такую годовую ставку ге, которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов, т.е. m = 1. Иными словами, схемы {Р, F1, r, m> 1} и {P, F1, re, m = 1} должны быть равносильными.
Из формулы (3.7) следует, что в рамках одного года
F1 =Р*(1+r/m)m.
Из определения эффективной годовой процентной ставки получается, что
F1=P*(1+re),
отсюда
ге =(1+r/m)m- 1. (3.13)
Из формулы (3.13) следует, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку; две эти ставки совпадают лишь при m = 1. Именно ставка rе является критерием эффективности финансовой сделки и может быть использована для пространственно-временных сопоставлений.
Пример
Предприниматель может получить ссуду: а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант более предпочтителен?
Относительные расходы предпринимателя по обслуживанию ссуды могут быть определены с помощью расчета эффективной годовой процентной ставки — чем она выше, тем больше уровень расходов. По формуле (3.13):
вариант (а):
rе = ( 1 + 0,26/12)12 — 1 = 0,2933, или 29,3%;
вариант (б):
гe = (1 + 0,27/2)2 — 1 = 0,2882, или 28,8%.
Таким образом, вариант (б) является более предпочтительным для предпринимателя. Необходимо отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель — эффективная ставка, а она, как следует из формулы (3.13), зависит лишь от номинальной ставки и количества начислений.
Понимание роли эффективной процентной ставки чрезвычайно важно для финансового менеджера. Принятие решения о привлечении средств, например банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предлагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки. Рассмотрим простейший пример.
Пример
Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%. По формуле (3.13):
| m. | ∞ | |||||
| гe | 0,10 | 0,1025 | 0,10381 | 0,10471 | 0,10516 | 0,10517 |
Различие между двумя ставками может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например при оформлении кредита на условиях добавленного процента.
Математически можно показать, что при m > 1 справедливо неравенство ге > г, которое, очевидно, следует и из финансовых соображений.
В финансовых соглашениях не имеет значения, какую из ставок указывать — эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же (с любой точностью приближения) наращенную сумму. В США в практических расчетах применяют номинальную ставку и, следовательно, формулу (3.7). В Европейских странах, как правило, вначале определяют эффективную ставку ге и затем пользуются формулой Fn = Р * (1 + ге )n.
Из формулы (3.13) следует, в частности, соотношение для определения номинальной ставки, если в контракте указаны эффективная годовая процентная ставка ге и число начислений сложных процентов m:
Сущность процентов и процентных ставок
ТЕМА 3. ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ
Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты, т.д.), либо от инвестиций производственного и финансового характера.
Процентная ставка – это величина, характеризующая интенсивность начисления процентов. Она определяется как отношение дохода, выплачиваемого за использование капитала в течение определенного периода времени к величине этого капитала.
Таким образом, величина получаемого дохода, то есть процентов, зависит от величины вкладываемого капитала, срока, на который он предоставляется в долг или инвестируется, размера и вида процентной ставки.
Множитель, или коэффициент наращения, — это величина, показывающая во сколько раз вырос первоначальный капитал.
Период начисления – это промежуток времени, за который начисляются проценты. Период начисления может разбиваться на интервалы начисления – это минимальный период по прошествии которого происходит начисление процентов.
Процентные ставки могут быть либо простыми, если они применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления, либо сложными,если по прошествии каждого интервала начисления они применяются к сумме долга и начисленных за предыдущие интервалы процентов.
В большинстве коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений или выплат в течение определенного периода. Такая последовательность называется потоком платежей.Поток однонаправленных платежей с равными интервалами между ними называется аннуитетом, или финансовой рентой.
Наиболее распространенные примеры аннуитета – регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам (аннуитет называется дивидендом).
Простые проценты применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления или когда после каждого интервала начисления кредитору выплачиваются проценты.
Введем следующие обозначения:
· П – проценты за весь срок
· Р – первоначальная сумма
· С – сумма, образовавшаяся к концу срока, или наращенная сумма
· А – ставка процентов в идее десятичной дроби
· n – число периодов
Процесс изменения суммы долга с наращенными простыми процентами описывается арифметической прогрессией:
Р
Р+Р*А=РР*(1+А)
Р*(1+А)+Р*А = Р*(1+2А)
С = Р*(1+n*А)
Это выражение называется формулой простых процентов, а множитель (1+n*А) – множителем наращения простых процентов.
Если срок начисления процентов меньше периода, на который установлена процентная ставка, то формула простых процентов приобретает вид:
С = Р*(1+Т/К*А),
где Т – число дней ссуды, К – число дней в году
За базу измерения времени часто берут год условно состоящий из 360-ти дней, то есть 12 месяцев по 3- дней. В этом случае вычисляют обыкновенный или коммерческий процент. В отличие от него точный процент получают, когда за базу берут действительное число дней в году 365 или 366. В свою очередь определения числа дней ссуды может быть точным или приближенным. В первом случае подсчитывается фактическое число дней между двумя датами, во втором продолжительность ссуды определяется количеством целых месяцев и дней ссуды, причем месяц принимается равным 30-ти дням.
В том и в другом случае дата выдачи и дата погашения считается за 1 день. В связи с этим применяется 3 варианта расчета:
· точные проценты с точным числом дней ссуды
· обыкновенные проценты с точным числом дней ссуды
· обыкновенные проценты с приближенным числом дней ссуды
Сложные проценты в настоящее время являются весьма распространенным видом процентных ставок, применяемых в различных финансовых операциях. Если после каждого интервала начисления доход не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулу сложных процентов.
Таким образом, наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления.
Рост по сложным процентам представляет собой процесс, развивающийся в геометрической прогрессии:
Р
Р+Р*А = Р*(1+А)
Р*(1+А)++Р*(1+А)*А = Р*(1+А)2
С = Р*(1+А)n
Это выражение называется формулой сложных процентов, а (1+А)n – множителем наращения сложных процентов.
Начисление сложных процентов может осуществляться на один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов – это годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.
При m равных интервалах начисления и номинальной процентной ставке An эта величина считается равной An/m. Тогда формула сложных процентов будет иметь вид:
С =
n – число лет ссуды
m – количество интервалов начислений в год
Можно определить годовую ставку сложных процентов, которая дает тот же финансовый результат, что и m разовое наращение в год по стае Аn/m – эта ставка называется эффективной и определяется:
Аэ = (1+An/m)m – 1
Часто встречаются ситуации когда финансовые контракты заключаются на период, отличающийся от целого числа лет. Если общее число интервалов начисления не является целым числом, то проценты могут начисляться одним из двух методов:
· по схеме сложных процентов:
С = Р*(1+An/m)n+l
· по смешанной схеме, когда для целого числа лет используется схема сложных процентов, а для дробной части года – схема простых процентов:
C = P*(1+An/m)n*m +P(1+l*An/m)
n – целое число лет, l – дробная часть года
Все рассмотренные выше проценты называются дискретными, так как их начисление осуществляется за фиксированный промежуток времени (год, месяц, квартал, день). В РФ этот вид начисления процентов является наиболее распространенным. В мировой практике также применяется так называемое непрерывное начисление сложных процентов, то есть когда продолжительность интервала начисления стремится к 0, а их количество к бесконечности. В РФ это способ начисления процентов практически не применяется.
Множественность способов начисления процентных ставок вызывает необходимость их корректного сопоставления. Для этого при расчетах, проводимых по различным финансовым операциям, определяются так называемые эквивалентные процентные ставки.
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты. Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент дл их сравнения.
Для нахождения эквивалентных процентных ставок используют уравнение эквивалентности, принцип составления которых заключается в следующем: выбирается величина, которую можно рассчитать при использовании различных процентных ставок. Обычно это наращенная сумма. На основе равенства двух выражений для данной величины составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.
Разница между простым процентом и сложным процентом
- 2019
Таким образом, простой процент — это сумма, выплачиваемая за использование заемных средств, за фиксированный период. С другой стороны, всякий раз, когда проценты подлежат уплате, они добавляются к основной сумме, по которой начисляются проценты за последующий период, это называется сложным процентом . Итак, здесь, в этой статье, вы найдете основные различия между простым интересом и сложным интересом, которые мы составили после углубленного исследования этих двух терминов.
Сравнительная таблица
| Основа для сравнения | Простой интерес | Сложный процент |
|---|---|---|
| Имея в виду | Простые проценты относятся к процентам, которые рассчитываются как процент от основной суммы. | Сложный процент относится к проценту, который рассчитывается как процент от основной суммы и начисленных процентов. |
| Вернуть | Меньше | Сравнительно высокий |
| принципал | постоянная | Продолжает меняться в течение всего периода заимствования. |
| рост | Остается однородным | Быстро увеличивается |
| Проценты начисляются на | принципал | Основной + накопленный интерес |
| формула | Простой интерес = P * r * n | Сложный процент = P * (1 + r) ^ nk |
Определение простого интереса
Простые проценты — это проценты, которые начисляются в процентах от первоначальной суммы, предоставленной или основной суммы, за весь период заимствования. Проценты — это цена, уплачиваемая за использование средств или доход, полученный от кредитования средств. Это самый простой и быстрый способ расчета процентов по сумме, одолженной или заемной. Наиболее распространенным примером простого интереса является автокредит, где проценты должны выплачиваться только на первоначальную сумму, одолженную или заимствованную. Следующая формула используется для расчета суммы процентов:
Формула : простой интерес = P × i × n
Где P = основная сумма
я = процентная ставка
n = количество лет
Например : если вы одолжите рупий. 1000 от вашего друга при 10% годовых в течение 3 лет, затем вы должны вернуть 1300 рупий своему другу в конце 3-го года 1000 рупий за основную сумму и рупий. 300 в качестве процентов, для хранения суммы при себе. Если мы сложим основную сумму и проценты, то она будет известна как сумма. Следует иметь в виду, что чем больше денег и периодов, тем выше будет процент.
Определение сложного процента
Сложный процент — это процент, который рассчитывается как процент от пересмотренного основного долга, то есть первоначального основного долга плюс накопленный процент за предыдущие периоды. В этом методе мы суммируем проценты, полученные в предыдущие годы, к первоначальной основной сумме, таким образом увеличивая основную сумму, с которой начисляются проценты за следующий период. Здесь проценты должны быть выплачены по основной сумме, а также проценты, начисленные в течение срока кредита.
Временной интервал между двумя периодами выплаты процентов называется Периодом конверсии. В конце конверсионного периода проценты начисляются следующим образом:
| Период конверсии | Составленный |
|---|---|
| 1 день | Ежедневно |
| 1 неделя | еженедельно |
| 1 месяц | ежемесячно |
| 3 месяца | квартальный |
| 6 месяцев | Раз в полгода |
| 12 месяцев | ежегодно |
Обычно банки выплачивают проценты раз в полгода, но финансовые учреждения проводят политику выплаты процентов ежеквартально. Для вычисления сложного процента вы должны использовать эту формулу:
Формула : сложный процент = P {(1 + i) n — 1}
Где P = принципал
n = количество лет
я = процентная ставка за период
Ключевые различия между простым интересом и сложным интересом
Ниже приведены основные различия между простым и сложным интересом:
- Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
- Сложный процент дает высокую доходность по сравнению с простым процентом.
- В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
- Темпы роста Простых процентов ниже, чем сложных процентов.
- Расчет простого процента прост, а расчет сложного процента сложен.
Видео: Простой против сложного интереса
пример
Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?
Решение : здесь P = 1000, r = 5% и t = 3 года
Простой интерес =

Сложный процент =
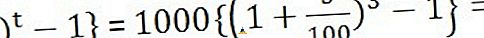
Заключение
Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.