Содержание
- Дисконтированная стоимость
- Наращение процентов и дисконтирование
- Дисконтированная стоимость денежных потоков
- Дисконтированная стоимость некоторых денежных потоков
- МСФО, Дипифр
- Номинальная
- Рыночная цена
- Как определить текущую?
- Формула расчета
- Выводы
- Дисконтированная стоимость перпетуитетов (бессрочных аннуитетов)
- Рыночная стоимость
- Курсовая цена
Дисконтированная стоимость
Дисконтированная (приведённая, текущая) стоимость — оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временно́й ценности денег). Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть другие факторы, снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.
Дисконтированная стоимость некоторой будущей суммы X {\displaystyle X} равна денежной сумме, при инвестировании которой сейчас (с доходностью, равной ставке дисконтирования), в будущем (в тот же момент времени) будет получена сумма X {\displaystyle X} . Дисконтированная стоимость потока платежей равна сумме дисконтированных стоимостей отдельных платежей, входящих в этот поток. Она фактически равна дисконтированной величине будущей стоимости денежного потока (сумма, которая будет получена в будущем, если денежный поток инвестировать в моменты получения платежей под ставку дисконтирования).
Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:
- доходности альтернативных вложений;
- стоимости привлечения (заимствования) средств;
- инфляции;
- срока, через который ожидается будущий поток платежей;
- риска, связанного с данным будущим потоком платежей;
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Наращение процентов и дисконтирование
Пусть некоторая денежная сумма P V {\displaystyle PV} вкладывается под ставку i {\displaystyle i} за единицу времени (день, месяц, квартал, год). Предполагается, что проценты начисляются и капитализируются в каждую единицу времени и фактически реинвестируются. Тогда в будущий момент времени t {\displaystyle t} будет получена сумма F V t {\displaystyle FV_{t}} , рассчитанная по формуле сложных процентов:
F V t = P V ( 1 + i ) t {\displaystyle FV_{t}=PV(1+i)^{t}}
Соответственно, если дана денежная сумма F V t {\displaystyle FV_{t}} на некоторый будущий момент времени t {\displaystyle t} , можно рассчитать сумму P V {\displaystyle PV} , которую нужно вложить под ставку i {\displaystyle i} , чтобы получить F V t {\displaystyle FV_{t}} к этому моменту, следующим образом:
P V = F V t ( 1 + i ) − t = F V t ( 1 + i ) t {\displaystyle PV=FV_{t}(1+i)^{-t}\,={\frac {FV_{t}}{(1+i)^{t}}}}
Величину PV называют дисконтированной (приведённой, текущей) стоимостью будущей суммы F V t {\displaystyle FV_{t}} , а ставку i {\displaystyle i} — ставкой дисконтирования. Саму операцию нахождения текущей стоимости будущей суммы называют дисконтированием.
В общем случае сумма может быть приведена к любому моменту времени (не только к текущему):
P V t 0 = F V t ( 1 + i ) t − t 0 {\displaystyle PV_{t_{0}}={\frac {FV_{t}}{(1+i)^{t-t_{0}}}}}
Приведение разновременных сумм к одному и тому же моменту времени делает их сопоставимыми (равноценными) с точки зрения концепции временно́й ценности денег. Предполагается, что существует возможность вложить любую сумму в любой момент времени в некоторый инструмент (например, банковский депозит) с доходностью i {\displaystyle i} . Природа инструмента несущественна, имеет значение только доходность при сопоставимом риске. В случае, если в качестве i {\displaystyle i} используется инфляция — это вложения в дорожающие товары и услуги. В качестве i {\displaystyle i} может выступать стоимость привлечения (заимствования) денег.
Пример
Если через 1 год ожидается сумма 121 рубль, то при ставке дисконтирования 10 % годовых дисконтированная стоимость будет равна 121 / ( 1 + 0 , 1 ) = 110 {\displaystyle 121/(1+0,1)=110} рублей. Если эта же сумма ожидается только через два года, то дисконтированная стоимость равна 121 / ( 1 + 0 , 1 ) 2 = 121 / 1 , 21 = 100 {\displaystyle 121/(1+0,1)^{2}=121/1,21=100} рублей.
В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.
Дисконтированная стоимость денежных потоков
Денежные потоки
Денежным потоком называют распределённое во времени движение денежных средств. Во многих случаях (депозиты, кредиты, ценные бумаги и др.) денежный поток представляет собой упорядоченную по времени совокупность денежных сумм (платежей) — это так называемый дискретный денежный поток или поток платежей. Таким образом, поток платежей C F = ( C F 1 , C F 2 , . . . . , C F n ) {\displaystyle CF=(CF_{1},CF_{2},….,CF_{n})} , где C F k {\displaystyle CF_{k}} — платёж, осуществляемый в момент времени t k {\displaystyle t_{k}} , k = 1.. n {\displaystyle k=1..n} . При этом формально n может быть также и бесконечным (бесконечный поток платежей). Если платежи осуществляются через равные промежутки времени, то иногда такой поток платежей называют финансовой рентой. Рента с постоянной величиной платежа называется аннуитетом (в некоторых источниках финансовая рента и аннуитет — эквивалентные понятия).
В некоторых случаях частота платежей может быть настолько большой, что денежный поток можно считать непрерывным. В частности, это имеет место для денежных потоков от обычной операционной деятельности компаний, потоков от инвестиционных проектов и т. д. Формально для непрерывных потоков можно ввести функцию плотности потока c ( t ) {\displaystyle c(t)} . Однако, на практике непрерывное время заменяется дискретным. А именно анализируемый период разбивается на равные периоды (месяц, квартал, год) и каждый период получает последовательный номер (это и есть дискретное время). Тогда денежный поток за каждый такой период C F t {\displaystyle CF_{t}} является фактически платежом в дискретный момент времени, соответствующий этому периоду. Таким образом непрерывный поток сводится, точнее моделируется как дискретный поток (поток платежей), описанный выше. Часто это интерпретируется также как платежи, осуществляемые в конце соответствующего периода — это так называемый поток постнумерандо. В некоторых случаях потоки рассматривают как платежи в начале каждого периода — поток пренумерандо.
Таким образом, можно считать, что денежный поток CF задаётся всегда упорядоченной совокупностью денежных сумм C F t {\displaystyle CF_{t}} — элементов денежного потока (платежей).
Дисконтированная стоимость потока платежей
Дисконтированная стоимость потока платежей C F = ( C F 1 , C F 2 , . . . . , C F n ) {\displaystyle CF=(CF_{1},CF_{2},….,CF_{n})} , где C F k {\displaystyle CF_{k}} — платёж, осуществляемый в момент времени t k {\displaystyle t_{k}} , k = 1.. n {\displaystyle k=1..n} , равна сумме дисконтированных стоимостей каждого из составляющих потока:
P V = ∑ k = 1 n C F k ( 1 + i ) t k {\displaystyle PV=\sum _{k=1}^{n}{{\frac {CF_{k}}{(1+i)^{t_{k}}}}\,}} Вывод формулы
Поток платежей разобьём на первый C F 1 {\displaystyle CF_{1}} и остальной ( C F 2 , C F 3 , . . . . ) {\displaystyle (CF_{2},CF_{3},….)} . Обозначим приведённую к моменту первой выплаты стоимость остаточного денежного поток P V 1 ∗ {\displaystyle PV_{1}^{*}} . Суммы C F 1 {\displaystyle CF_{1}} и P V 1 ∗ {\displaystyle PV_{1}^{*}} относятся к одному моменту времени и их можно привести к текущему моменту делением на ( 1 + i ) t 1 {\displaystyle (1+i)^{t_{1}}}
P V 0 = C F 1 ( 1 + i ) t 1 + P V 1 ∗ ( 1 + i ) t 1 {\displaystyle PV_{0}={\frac {CF_{1}}{(1+i)^{t_{1}}}}+{\frac {PV_{1}^{*}}{(1+i)^{t_{1}}}}}
Аналогичным образом можно разделить остаточный поток на платёж C F 2 {\displaystyle CF_{2}} и оставшийся после t 2 {\displaystyle t_{2}} поток и получим
P V 1 ∗ = C F 2 ( 1 + i ) t 2 − t 1 + P V 2 ∗ ( 1 + i ) t 2 − t 1 {\displaystyle PV_{1}^{*}={\frac {CF_{2}}{(1+i)^{t_{2}-t_{1}}}}+{\frac {PV_{2}^{*}}{(1+i)^{t_{2}-t_{1}}}}}
Подставив это в первую формулу получим
P V 0 = C F 1 ( 1 + i ) t 1 + C F 2 ( 1 + i ) t 2 + P V 2 ∗ ( 1 + i ) t 2 {\displaystyle PV_{0}={\frac {CF_{1}}{(1+i)^{t_{1}}}}+{\frac {CF_{2}}{(1+i)^{t_{2}}}}+{\frac {PV_{2}^{*}}{(1+i)^{t_{2}}}}}
Поступая аналогичным образом и далее до последнего платежа, окончательно получим формулу дисконтированной стоимости всего денежного потока
P V = ∑ k = 1 n C F k ( 1 + i ) t k {\displaystyle PV=\sum _{k=1}^{n}{\frac {CF_{k}}{(1+i)^{t_{k}}}}}
Интерпретация
При вложении суммы P V {\displaystyle PV} на период до t >= t n {\displaystyle t>=t_{n}} под ставку i {\displaystyle i} будет в конечном итоге получена сумма:
F V = P V ∗ ( 1 + i ) t = ∑ k = 1 n C F k ( 1 + i ) t − t k {\displaystyle FV=PV*(1+i)^{t}=\sum _{k=1}^{n}CF_{k}(1+i)^{t-t_{k}}}
Таким образом, эта сумма равна сумме, которая будет получена в этот же момент, если последовательно под ту же ставку вкладывать отдельные элементы потока до времени t. Таким образом, дисконтированная стоимость денежного потока равна дисконтированной стоимости наращенной суммы этого потока.
Если платежи осуществляются через равные промежутки времени, то формулу можно записать без дополнительного индекса нумерации платежей k {\displaystyle k} . Время t {\displaystyle t} и будет представлять просто номер платежа:
P V = ∑ t = 1 n C F t ( 1 + i ) t {\displaystyle PV=\sum _{t=1}^{n}{\frac {CF_{t}}{(1+i)^{t}}}}
Необходимо отметить, что в этих формулах время измеряется в единицах периода ставки дисконтирования i. Обычно ставка даётся годовая, а время может быть дано в днях, месяцах, кварталах и т. д. В этом случае в качестве времени необходимо использовать отношение времени в заданных единицах к продолжительности года в тех же единицах (например, если выплата через квартал, то это 0,25 года). Если платежи осуществляются через равные промежутки времени можно пересчитать ставку на этот период по формуле сложных процентов: i ′ = ( 1 + i ) 1 / T − 1 {\displaystyle i’=(1+i)^{1/T}-1} , где T — продолжительность года в единицах этого периода (например для ежемесячного платежа — это 12, для ежеквартального — 4 и т. д.).
Имеется облигация номиналом в 1000 рублей со сроком до погашения 1 год и ежеквартальным купоном 20 рублей, что соответствует купонной ставке 8 % годовых (20 x 4 / 1000 = 0,08). Владелец облигации получает в первые три квартала по 20 рублей, а в четвёртом квартале — 20 рублей и сумму погашения. Таким образом, структура выплат следующая: 20 + 20 + 20 + 1020. Периоды между платежами равные.
Теперь продисконтируем данный поток платежей. Допустим, ставка дисконтирования равна 6,14 % годовых (например, это ожидаемая инфляция или 5,5 % безрисковая ставка плюс премия за риск 0,64 % для инструментов с данным риском — цифра условная для примера). Можно посчитать квартальную ставку как 1 , 0614 1 / 4 − 1 {\displaystyle 1,0614^{1/4}-1} получаем примерно 1,5 % в квартал. Таким образом, дисконтированная стоимость данного потока платежей при квартальной ставке в 1,5 % будет равна
То же самое можно рассчитать непосредственно через годовую ставку, не рассчитывая квартальную ставку, а используя время в долях от года:
Дисконтированная стоимость некоторых денежных потоков
Дисконтированная стоимость аннуитета
Если поток платежей аннуитетный, то есть платежи имеют одинаковую величину и выплачиваются через равные промежутки времени, то эта формула принимает вид (исходя из известной формулы суммы геометрической прогрессии):
P V = C F i ⋅ = C F ⋅ 1 − ( 1 + i ) − n i {\displaystyle PV\,=\,{\frac {CF}{i}}\cdot \,=\,CF\cdot {\frac {1-(1+i)^{-n}}{i}}} ,
где C F {\displaystyle CF} — аннуитетный платёж, осуществляемый n {\displaystyle n} раз; i {\displaystyle i} — ставка дисконтирования; P V {\displaystyle PV} — дисконтированная стоимость аннуитетных платежей C F {\displaystyle CF} .
Дисконтированная стоимость вечных аннуитетов (перпетуитетов)
Для вечного аннуитета, то есть при бесконечно большом n {\displaystyle n} , выражение в квадратных скобках в формуле дисконтированной стоимости аннуитета, становится равным единице, поэтому формула ещё более упрощается:
P V = C F i {\displaystyle PV\,=\,{\frac {CF}{i}}}
Дисконтированная стоимость платежей с постоянным темпом роста
Если платежи растут с постоянным темпом прироста g, то их дисконтированная стоимость вычисляется по формуле:
P V = C F 1 i − g {\displaystyle PV\,=\,{CF_{1} \over i-g}\left} ,
где C F 1 {\displaystyle CF_{1}} — платёж, осуществляемый в первый период, n {\displaystyle n} — число периодов, i {\displaystyle i} — ставка дисконтирования.
В пределе (при бесконечно большом n) при g < i {\displaystyle g<i} получается следующая простая формула (модели Гордона):
P V = C F 1 i − g {\displaystyle PV\,=\,{CF_{1} \over i-g}}
МСФО, Дипифр
 Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.
Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов. Ваши 1000 долларов, положенные в банк сегодня, при банковской ставке 10% будут стоить 1100 долларов завтра: нынешние 1000 долларов + проценты по вкладу 100 (=1000*10%). Итого через год вы сможете снять 1100 долларов. Если выразить этот результат через простую математическую формулу, то получим: $1000*(1+10%) или $1000*(1,10) = $1100.
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента. Чем она больше, тем быстрее растет вклад. Если бы ставка банковского процента была другой, например, 12%, то через два года вы бы смогли снять с вклада примерно 1250 долларов, а если считать более точно 1000*(1,12)2 = 1254.4
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.
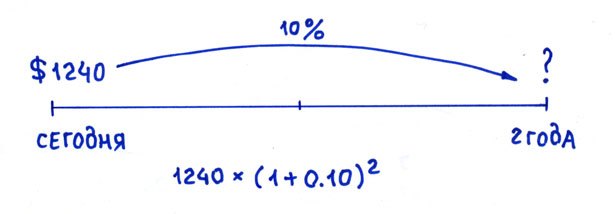
Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210. Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
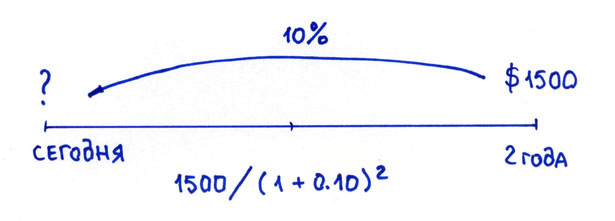
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
 Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)n называется фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.
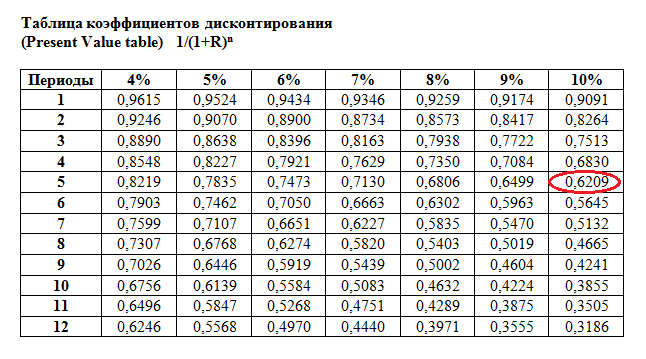
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это таблица коэффициентов дисконтирования, которые рассчитываются, как правило, с точностью до четвертого знака после запятой.
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
|
сегодня |
через 5 лет |
|
62,09 цента |
|
|
X? |
150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)5 = 161,050 долларов. Это более выгодный вариант.
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n .
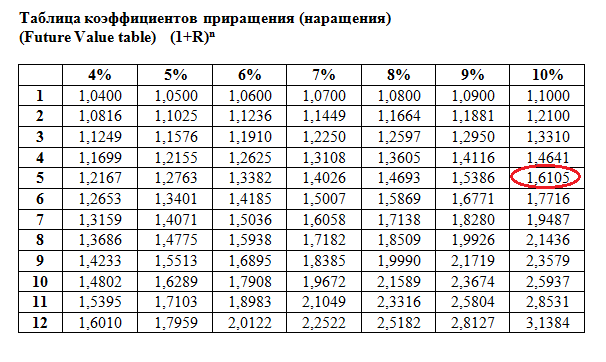 Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Номинальная
Номинальная стоимость — это цена облигации, с которой она «родилась». Номинал представляет собой сумму, обозначенную эмитентом, выпустившим бумагу: компанией, печатающей облигации, государством в лице Минфина, продуцирующим долговые бумаги для привлечения вкладов населения в развитие экономики.
Иными словами, это базовая стоимость, на основании которой происходят все дальнейшие расчёты.
![]() Для разных типов бумаг в процессе размещения назначается своя «номиналка». Например, облигации федерального займа (ОФЗ — это государственные долговые бумаги) выпускаются с номиналом 1000 рублей за одну единицу. Покупают обычно в больших количествах, но никто не запрещает купить даже одну штуку. Эта сумма удобна всем и в дальнейших расчётах процентного дохода. Большинство отечественных бондов, вращающихся на биржевых площадках, имеют именно эту стоимость. Но, бывают облигации и с номиналом 10, 50, 200 тыс. рублей или даже 2 миллиона за одну бумагу.
Для разных типов бумаг в процессе размещения назначается своя «номиналка». Например, облигации федерального займа (ОФЗ — это государственные долговые бумаги) выпускаются с номиналом 1000 рублей за одну единицу. Покупают обычно в больших количествах, но никто не запрещает купить даже одну штуку. Эта сумма удобна всем и в дальнейших расчётах процентного дохода. Большинство отечественных бондов, вращающихся на биржевых площадках, имеют именно эту стоимость. Но, бывают облигации и с номиналом 10, 50, 200 тыс. рублей или даже 2 миллиона за одну бумагу.
Обратите внимание, что номинал — заимствованная у вкладчика сумма, которая подлежит возврату по истечении срока облигационного займа. Именно её вы гарантированно получите на руки в дату погашения ценной бумаги.
Рыночная цена
 Итак, рыночная стоимость облигации — это цена, по которой продаётся бумага на вторичном рынке, после проведения первичных торгов. Рыночная цена выражается в процентах от номинальной. Например, если она равна 103%, а номинал 1000 рублей, то за такую облигацию придётся отдать 1030 рублей. Бывает и такое, что она ниже номинала, например, 97%. Обычно говорят, что это цена с дисконтом или дисконтная. В этом случае бумагу можно купить дешевле, за 970 рублей соответственно.
Итак, рыночная стоимость облигации — это цена, по которой продаётся бумага на вторичном рынке, после проведения первичных торгов. Рыночная цена выражается в процентах от номинальной. Например, если она равна 103%, а номинал 1000 рублей, то за такую облигацию придётся отдать 1030 рублей. Бывает и такое, что она ниже номинала, например, 97%. Обычно говорят, что это цена с дисконтом или дисконтная. В этом случае бумагу можно купить дешевле, за 970 рублей соответственно.
В отличие от строго определённых изначально: цены по номиналу, эмиссионной стоимости и цены погашения, рыночная стоимость бонда изменчива, как погода в Англии.
Она определяется положением дел, которое сложилось на рынке данных активов и на финансовых просторах в целом на момент продажи.
«Температура» цен на бирже во время торгов меняется в зависимости от таких «атмосферных» воздействий:
- спрос (много ли покупателей желают заполучить активы);
- предложения на рынке (возможно есть более выгодные);
- срока, который остался до погашения;
- уровня процентной ставки;
- возможности получать от бонда регулярный фиксированный доход;
- существующих рисков
- и прочего, и прочего…
Как определить текущую?
Если мы хотим участвовать в торгах по нашим облигациям, необходимо постоянно быть в курсе ситуации в «финансовой мекке» и следить за движением рыночных цен на интересующие активы.
Рыночную стоимость удобно просматривать, скачав на свой компьютер специальную программу QUIK.
Этот клиентский торговый терминал является многофункциональным аналогом рабочего места биржевого трейдера. Он имеет все необходимые нам сведения и применяется для проведения как простых и доступных каждому операций, так и для специализированных целей. Поэтому весьма популярен.
На картинке ниже, мы показали как это выглядит в QUIK. Текущая рыночная стоимость облигации в QUIK — это столбец «Цена последней сделки». Два раза кликнув по бумаге, можно открыть биржевой стакан. Если мы хотим сразу купить, то смотрим на красненькие заявки (продавцы), самую маленькую цену (она вверху). Если продаём, смотрим на зелёный столбец покупателей — самую высокую предлагаемую цену (внизу).
Столбец с рыночной стоимостью государственных ОФЗ и стакан с заявками одной из бумаг
Обратите внимание: вход в QUIK возможен только после оформления брокерского счета и подключения к системе с получением данных для входа. Узнать конечные стоимости на момент закрытия торговой сессии прошлого дня (итоги торгов) можно и на специальных сайтах.
Одним из таких сайтов является rusbonds.ru. Там требуется регистрация для просмотра подробных сведений о бумаге, но она бесплатная и ничего не требует. Перейдя на сайт, воспользуйтесь поиском нужной бумаги и перейдите на страницу облигации, там во вкладке «Общие сведения» ищите «итоги торгов».
Стрелочкой показано где смотреть текущую рыночную цену на rusbonds
Без регистрации можно посмотреть цены на сайте брокера Финам. Для этого перейдите в раздел «Облигации» → «Итоги торгов». Затем найдите интересующую облигацию и перейдите на её страницу. Там можно найти цену также во вкладке «Итоги торгов».
Выбрана вкладка Т+, потому что рассматриваемая бумага торгуется в этом режиме
Обратите внимание на 3 цены, давайте переведем. Во-первых, это цены на момент закрытия торговой сессии за предыдущий день. Close — это цена последней совершенной сделки. Bid — это самая большая цена, за которую покупатель выставил заявку в биржевом стакане, т.е. готов купить по этой цене, если это устроит продавца. Ask — это минимальная цена, которую выставил владелец облигаций на продажу.
Формула расчета
Теперь, разобравшись во всех понятиях, давайте определим формулу для расчета цены облигации. Именно той цены, которую платит покупатель, приобретая бумагу на вторичном рынке.
ЦенаПокупки = n * (НомРуб * РынЦен%) + n * НКД, где
- n — это количество облигаций;
- НомРуб — номинал бумаги в рублях;
- РынЦен — рыночная цена в процентах;
- НКД — накопленный купонный доход.
Для большего понимания, рассмотрим реальный пример на одной из ОФЗ. У неё следующие параметры: Номинал = 1000 рублей, рыночная стоимость 103.8%, НКД = 32.38 (большое значение, но скоро выплата купона, который составляет 40.64 рублей). Допустим, мы хотим купить 200 облигаций.
По нашей формуле, получим:
Цена покупки = 200 * (1000 * 103.8%) + 200 * 32.38 = 200 * 1038 + 6476 = 214 076 рублей.
Итого, чтобы купить 200 облигаций с номиналом 1000 рублей, пришлось заплатить на целых 14 тыс. больше. Мало того, что цена выше номинала, так ещё и НКД высокий. Но на самом деле это хорошая бумага, которая даёт почти 8% годовых. Так, примерно через месяц у неё будет выплата купона, за который мы уже получим 200 * 40.64 = 8128 рублей обратно. И будем получать такой купон ещё долго, до срока погашения, который через 9 лет. Если мы захотим продать её раньше, покупатель также заплатит нам и рыночную стоимость и НКД, как это сделали мы по этой формуле.
Выводы
Используя облигации в качестве источника прибыли, учитываем следующие моменты:
- Эти ценные бумаги обладают различными видами стоимости в разный период времени и торгуются по рыночной цене.
- Отправной точкой вычислений цен на бонды в границах биржевых торгов является их номинал.
- При покупке и продаже облигаций, необходимо учесть, что она может содержать «привесок» в виде накопленного купонного дохода.
Приняв решение зарабатывать на бондах, следите за ходом биржевых процессов, используя торговые терминалы. Таким образом, вы сможете контролировать котировки ценных бумаг и выигрывать на их купле-продаже.
Хорошей доходности капиталовложений!
2908 просмотров Поставьте оценку статье и помогите стать лучше: 4.000 / 5 (5 голосов) – честный рейтинг статьи от читателей. Заметили ошибку в тексте? Пожалуйста, выделите её и нажмите Ctrl + Enter Понравилась статья? Поделись с друзьями:
Дисконтированная стоимость выражает стоимость будущих потоков платежей в значении текущих потоков платежей. Определение дисконтированной стоимости широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений намерен сделать инвестор для получения определённого денежного потока через заданный срок. Дисконтированная стоимость будущего потока платежей является функцией:
- инфляции,
- срока, через который ожидается будущий поток платежей,
- риска, связанного с данным будущим потоком платежей,
- стоимости денег с учётом фактора времени,
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Дисконтированная стоимость перпетуитетов (бессрочных аннуитетов)
Исходя из формулы расчета дисконтированной стоимости аннуитетных платежей, можно получить формулу для дисконтированной стоимости перпетуитетов (бессрочных аннуитетов). Когда значение стремится к бесконечности, часть формулы , стремится к нулю. При таких условиях формула для перпетуитетов будет иметь следующий вид:
.
Дисконтированная стоимость бессрочных ценных бумаг с растущими платежами, например акции, с увеличивающимися дивидендными доходами, рассчитывается по модели Гордона.
Дисконтированная стоимость (Discounted cash flow, DCF) – это приведенная стоимости будущих (ожидаемых) денежных платежей к текущему моменту времени. Дисконтирование денежных потоков основывается на важном экономическом законе убывающей стоимости денег. Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (снижается покупательная способность денег, т.е. на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть и другие факторы снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.
Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объем финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:
- доходности альтернативных вложений;
- стоимости привлечения (заимствования) средств;
- инфляции;
- срока, через который ожидается будущий поток платежей;
- риска, связанного с данным будущим потоком платежей;
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Процесс дисконтирования стоимости осуществляется как по простым, так и по сложным процентам.
При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:
где Д — сумма дисконта, определенная по простым процентам за обусловленный период времени в целом;
S — будущая стоимость денежных средств (финансового инструмента);
n — количество отдельных периодов, по которым предусматривается расчет процентных платежей;
i — используемая дисконтная ставка, выраженная десятичной дробью.
В этом случае настоящая стоимость денежных средств (финансового инструмента) с учетом рассчитанной суммы дисконта определяется по формулам:
или
где Р — настоящая стоимость денежных средств (финансового инструмента);
S — будущая стоимость денежных средств (финансового инструмента);
Д — сумма дисконта, определенная по простым процентам;
n — количество отдельных периодов, по которым предусматривается расчет процентных платежей в общем обусловленном периоде времени;
i — используемая дисконтная ставка, выраженная десятичной дробью.
При расчете настоящей стоимости денежных средств в процессе их дисконтирования по сложным процентам используется следующая формула:
где Рс — настоящая стоимость денежных средств (финансового инструмента), дисконтированная по сложным процентам;
S — будущая стоимость денежных средств (финансового инструмента);
n — количество отдельных периодов, по которым предусматривается расчет процентных платежей в общем обусловленном периоде времени;
i — используемая дисконтная ставка, выраженная десятичной дробью.
Соответственно сумма дисконта в этом случае определяется по формуле:
Дс = S — Рс
где Дс — сумма дисконта, определенная по сложным процентам за обусловленный период времени в целом;
S — будущая стоимость денежных средств (финансового инструмента);
Рс — настоящая стоимость денежных средств (финансового инструмента), дисконтированная по сложным процентам.
Множитель называется множителем дисконтирования стоимости по сложным процентам.
Рыночная стоимость
Денежная стоимость ЦБ такой ссуды в свободной продаже в период между первичным размещением и погашением является их рыночной оплатой. Она может совпадать с номиналом, а также быть ниже или выше него (покупка с дисконтом или с премией соответственно) и в свою очередь подразделяется на «грязную» и «чистую», то есть стоимость с учетом накопленного купонного дохода и без такового. Ниже даны формулы расчета, по которым можно определить, сколько стоит в текущий момент каждый из наиболее часто встречающихся в практике видов бумаг облигационных займов без учета накопленного купонного дохода.
Расшифровка обозначений, фигурирующих в формулах:
- N – номинал;
- P – рыночная стоимость;
- g – годовая % ставка по купону;
- C=g × N – годовой % доход по купону;
- i – ставка доходности к погашению (ставка помещения, полной доходности, дисконтирования);
- n – время в годах, оставшееся до даты погашения.
Стоимость облигаций с нулевым купоном:
P= N/〖(1+i)〗^n
Характеристика ссуды: регулярный % доход отсутствует, а вся прибыль получается за счет дисконта между номиналом при выкупе покупки.
Стоимость облигаций с выплатой % по купону при погашении:
P= (N ×〖(1+g)〗^n)/〖(1+i)〗^n
Характеристика ссуды: купон начисляется по сложной ставке процента и выплачивается одновременно с номиналом при выкупе.
Стоимость облигаций с фиксированным % по купону:
P=C × (1- 1/〖(1+ i)〗^n )/i + N/〖(1+ i)〗^n
Характеристика ссуды: периодическая выплата купонного % с фиксированной ставкой и номинала в момент выкупа.
Стоимость облигаций с плавающим процентом по купону:
P= ∑_(k=1)^n▒〖C_k/〖(1+i)〗^k + N/〖(1+i)〗^n 〗 ,
где C_k – годовой купонный доход за определенный период, а k – время в годах, оставшееся до выплаты соответствующего купона.
Характеристика ссуды: купонный процент является переменным и привязан к какому-либо показателю, ставка по купону объявляется перед началом очередного периода, номинал выплачивается в момент погашения.
Стоимость бессрочной облигаций с периодической выплатой процентов:
P = C/i
Характеристика ссуды: периодическая выплата купонного %, конкретные сроки выкупа номинала отсутствуют, поэтому облигационная ссуда носит характер так называемой вечной ренты.
Если же необходимо рассчитать, сколько стоит в данный момент облигация с учетом накопленного купонного дохода НКД, то его необходимо приплюсовать к уже рассчитанной текущей стоимости:
P_g = P_с+ C_t ,
где C_t – НКД, а P_g и P_с – цена с учетом НКД и без него соответственно.
НКД определяется по формуле:
C_t = C ×( 1/m-t) ,
где m – годовое количество платежей по купонам, t – время до платежа по очередному купону (в годовом исчислении).
Как мы видим, во всех приведенных уравнениях есть одна общая переменная, напрямую влияющая на стоимость облигаций. Это ставка доходности к погашению. Что она собой представляет и от чего зависит? Упомянутая ставка определяет, под сколько % инвестор реально вкладывает в текущий момент свои денежные средства с учетом всех видов дохода. На нее влияют следующие параметры:
- процентная ставка по купону;
- частота выплат купонного дохода;
- рыночная ставка %;
- степень надежности финансовых вложений;
- срок до погашения;
- возможность досрочного выкупа;
- налоговый статус.
Курсовая цена
Для удобства в сопоставлении текущей рыночной стоимости облигаций в практику был введен общий показатель, который называется курсовая цена, или просто курс. При операциях купли-продажи именно курс обычно служит основой для котировок и одной из инвестиционных характеристик. Под ним понимают рыночную стоимость 100 единиц номинала, поэтому формула довольно простая:
K= P/N × 100
Через ставку помещения курс выражается следующим соотношением:
K= 100/〖(1+i)〗^n
В некоторых случаях, например, при торговле бумагами муниципальных займов в США, котировки определяются не на основе курса, а на базе текущей ставки помещения.
Итак, в нашем кратком обзоре мы разобрались с расчетом цены облигаций и выяснили, сколько видов ее существует и что все они вовсе не тождественны друг другу. Правильное понимание того, о какой из них А идет речь в каждой конкретной ситуации, важно с практической точки зрения, особенно при заключении сделки, так как любые разночтения и неверная трактовка термина могут быть чреваты неприятными финансовыми последствиями и прямыми убытками.
Метод рыночных процентов состоит в том, что постоянная рыночная ставка процента (рыночная ставка на момент выпуска облигаций) применяется к текущей стоимости облигации на начало периода выплаты процентов (умножается), что дает величину расходов на выплату процентов. Доля амортизации дисконта (премии) рассчитывается как разница между полученной величиной и реальной суммой процентов, выплачиваемых держателю облигации.
Чистая текущая стоимость облигации
Поскольку это эквивалентные ценные бумаги, в соответствии с законом единой цены текущая стоимость облигации в иенах, выраженная в долларах, должна быть равна текущей стоимости в долларах для синтетической облигации в иенах. Таким образом, мы приходим к уравнению паритета между форвардными и спот курсами для доллара и иены
Оценка облигации с купоном с постоянным уровнем выплат. Когда купонные платежи процентов фиксированы, оценщик имеет дело с простым процентным обязательством и постоянные процентные платежи он может рассматривать как аннуитет. Текущая стоимость облигации в этом случае состоит из двух частей
Текущей дисконтированной стоимости выплаты номинала при наступлении срока погашения облигации. Формула определения текущей стоимости облигации имеет следующий вид
FV — текущая стоимость облигаций, ден. ед. Y — годовые процентные выплаты, определяющиеся номинальным процентным доходом (купонной ставкой)
Необходимо определить текущую стоимость облигации с оставшимся сроком погашения 6 лет, номинальной стоимостью 100000 руб., приносящей 6%-ный купонный доход при требуемом уровне доходности 10%.
Текущая стоимость облигации равна 82530 руб. (56400+26130).
Текущая стоимость облигации равна 110452 руб. (79000+31452).
Пример. Оценить текущую стоимость облигации нарицательной стоимостью 200000 руб., купонной ставкой 15% годовых и сроком погашения через 5 лет, если рыночная норма дохода 12%. Процент по облигации выплачивается дважды в год.
Текущая стоимость облигации равна 222000 руб. (110400+111600).
Облигация через год будет погашена по номиналу 100 ден. ед. из расчета 10% годового дохода по ней. Следовательно, текущая стоимость облигации или цена, по которой она может быть продана в настоящее время, равна PV= 100/ (1+0,1)=90,9 ден. ед.
Если при тех же условиях облигация будет погашена через три года, ее текущая стоимость составит PV= 0/(1+0,1) +0/(1+0,1)2 +100/(1+0,1)3 = 0/1,1+ 0/ 1,21 + 100/1,331=75,13 ден. ед. Если в первые два года будут проводиться купонные выплаты по 5 ден. ед., текущая стоимость облигации составит PV= 5/ 1,1+ 5/1,21+ 100/1,331=4,54+ 4,13+ 75,13=83,8 ден. ед.
Пример. Пусть инвестору необходимо определить текущую стоимость облигации номиналом 1 000,0 тыс. руб., ставкой купонного дохода 30% и сроком обращения 10 лет, которая бы обеспечила ему получение 35% годового дохода (на уровне рыночной нормы доходности).
Подставляя эти величины в формулу текущей стоимости облигации, получим I
По 5,5%-ной купонной облигации номиналом 200 долл. обещают производить купонные платежи каждые полгода. Определить текущую стоимость облигации если до ее погашения остается 2 года, а безрисковые процентные ставки при непрерывном начислении равны
Найти текущую стоимость облигации, когда до очередного купонного платежа остается 4 мес., если значение ставки-ориентира в начале первого купонного периода было 7,5%, а ставка дисконтирования на 4 мес. равна 7% (при непрерывном начислении).
Найти текущую стоимость облигации, если значение ставки-ориентира в начале первого купонного периода было 8%, а подходящие ставки дисконтирования при непрерывном начислении на 2, 5, 8 и 11 мес. равны 10,0 10,2 10,5 11,00 % соответственно.
Определить текущую стоимость облигации, если она может быть
Определить текущую стоимость облигации, если в нее встроен
Найти текущую стоимость облигации при условиях задачи 25.1, если до ее погашения остается 2 года. Определить размер премии за дефолт-риск, выплачиваемой держателям облигации.
Процентная ставка, используемая на рынке для дисконтирования выкупной цены облигации, является спот-ставкой соответствующего периода до погашения. Однако эта спот-ставка не фигурирует во время торгов на рынке, определяется лишь текущая цена облигаций с нулевым купоном. Спот-ставку можно рассчитать, зная текущую стоимость облигации, из следующего уравнения
Облигация с нулевым купоном — это облигация, по которой не выплачиваются периодические процентные платежи (известные как купоны) в течение срока ее обращения, отсюда и термин «нулевой купон». Этот вид облигаций выпускается и обращается с дисконтом, так как единственный ожидаемый будущий денежный поток — это номинальная или выкупная цена облигации в конце срока обращения. Доход образуется за счет разницы между текущей стоимостью облигации в момент ее эмиссии или приобретения и стоимостью в момент погашения или продажи. Таким образом, настоящей (текущей) стоимостью или ценой данных облигаций является текущая стоимость выкупного платежа. Формула для расчета текущей стоимости облигации следующая
Текущая стоимость облигаций. Факторы, воздействующие на вола-тильность облигации. Длительность (дюрация). Дюрация бескупонных и купонных облигаций. Оценка риска с помощью дюрации. Цель и принципы формирования портфеля из облигаций. Стратегия облигационного портфеля. Иммунизация портфеля. Управление портфелем из ГКО, ОФЗ, ОГСЗ.
Вылаченная сумма процентов по облигациям Текущая стоимость облигаций
В соответствии с методом рыночных процентов применяется постоянная рыночная ставка процента (effe tive rate) к текущей стоимости облигаций. В результате суммы списываемого дисконта или премии и соответственно доходы в виде процентов изменяются каждый период. Американские стандарты рекомендуют использовать данный метод, так как он более точно увязывает доходы и расходы периода.
Каждый индекс рассчитывается по гипотетическому портфелю, включающему, например, 23 вида швейцарских облигаций. При расчете индексов за 100% принимается величина соответствующего портфеля на конец 1982 г. Стоимость портфеля Value ) основана на текущей стоимости облигаций плюс доход от реинвестирования начисленных процентов. Из приведенных данных видно, что при увеличении стоимости портфеля (росте курса облигаций) его доходность к погашению уменьшается.
Пример. Пусть инвестору необходимо определить теку цую стоимость облигации номиналом 1 000,0 тыс. руб. и сроком обращения пять лет при условии, что ожидаемая норма доходности составит 20% годовых. Г од-ставляя значения в формулу текущей стоимости облигации, получим
Дана купонная облигация со следующими данными А = 100 долл., /= 10%, т — 1, Т = 3 года. Текущая стоимость облигации равна 102J долл. Ожидаемый средний годовой темп инфляции — 4%.